题目内容
类比学习:
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,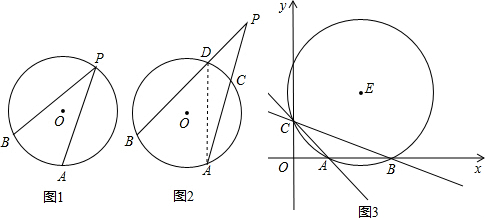
新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=
归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于
新知应用:
直线y=-x+m与直线y=-
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
我们已经知道,顶点在圆上,且角的两边都和圆相交的角叫做圆周角,如图1,∠APB就是圆周角,弧AB是∠APB所夹的弧.
类似的,我们可以把顶点在圆外,且角的两边都和圆相交的角叫做圆外角,如图2,∠APB就是圆外角,弧AB和弧CD是∠APB所夹的弧,

新知探索:
图(2)中,弧AB和弧CD度数分别为80°和30°,∠APB=
25
25
°,归纳总结:
(1)圆周角的度数等于它所夹的弧的度数的一半;
(2)圆外角的度数等于
所夹两弧的度数差的一半
所夹两弧的度数差的一半
.新知应用:
直线y=-x+m与直线y=-
| ||
| 3 |
设∠APC=θ.
①求A点坐标; ②求⊙E的直径;
③连接MN,求线段MN的长度(可用含θ的三角函数式表示).
分析:新知探索:
根据弧AB和弧CD度数分别为80°和30°,得出∠BDA=40°,∠DAC=15°,再利用三角形外角的性质求出∠APB即可;
归纳总结:
根据由图2所求∠APB的度数,进而求出圆外角的度数等于所夹两弧的度数差的一半,
新知应用:
①直线y=-
x+2与y轴的交点可以求出,把这点的坐标就可以求出直线y=-x+m的解析式,两个函数与x轴的交点就可以求出;
②根据三角函数可以求出角的度数.根据OC、OA、OB的长度根据三角函数可以根据三角函数求出角的度数;
③根据正弦定理就可以解决.
根据弧AB和弧CD度数分别为80°和30°,得出∠BDA=40°,∠DAC=15°,再利用三角形外角的性质求出∠APB即可;
归纳总结:
根据由图2所求∠APB的度数,进而求出圆外角的度数等于所夹两弧的度数差的一半,
新知应用:
①直线y=-
| ||
| 3 |
②根据三角函数可以求出角的度数.根据OC、OA、OB的长度根据三角函数可以根据三角函数求出角的度数;
③根据正弦定理就可以解决.
解答:解:新知探索:
∵弧AB和弧CD度数分别为80°和30°,
∴∠BDA=40°,∠DAC=15°,
∴∠APB=∠BDA-∠DAC=15°,
故答案为:25;
归纳总结:
(2)根据上面所求可以得出:圆外角的度数等于所夹两弧的度数差的一半,
故答案为:所夹两弧的度数差的一半;
新知应用:
①直线y=-
x+2中令x=0,
解得y=2,因而C点的坐标是(0,2),
把(0,2)代入直线y=-x+m,
解得m=2,
∴解析式是y=-x+2,
令y=0,解得x=2,则A点的坐标是(2,0),
②在y=-
x+2中令y=0,
解得x=2
,则B的坐标是(2
,0);
根据A、B、C的坐标得到OC=2,OA=2,OB=2
,
根据三角函数得到:tan∠CBO=
=
,
故∠ABC=30°.
如图1,连接AE,CE,过点E作EW⊥y轴于点W,ET⊥x轴于点T,
则∠AEC=60°,
∴△ACE是等边三角形,边长是2
,
∵∠WCE=180°-∠OCA-∠ECA=75°,
∠EAT=180°-∠CAO-∠EAC=75°,
∴∠WCE=∠EAT,
在△WCE和△TAE中,
,
∴△WCE≌△TAE,
∴WE=ET,
∵ET⊥AB,
∴AT=BT,
∵AB=OB-OA=2
-2,
∴AT=
-1,
∴OT=
+1,故ET=
+1,
因而E的坐标是(
+1,
+1),
故AE=
=2
,
即半径是2
,故⊙E的直径为4
,

③如图2所示:MN为⊙E中任一弦,它对的圆周角为∠B,当AM为直径,
则∠ANM为直角,则sinB=sinA=
,
即MN=AM•sinA①(其实就是正弦定理),
根据点P在⊙E外,如图3,连接AN,
则∠MAN=∠ANC-∠P=∠ABC-∠P=30°-θ,
由①得:MN=4
sin(30°-θ).
∵弧AB和弧CD度数分别为80°和30°,
∴∠BDA=40°,∠DAC=15°,
∴∠APB=∠BDA-∠DAC=15°,
故答案为:25;
归纳总结:
(2)根据上面所求可以得出:圆外角的度数等于所夹两弧的度数差的一半,
故答案为:所夹两弧的度数差的一半;
新知应用:
①直线y=-
| ||
| 3 |
解得y=2,因而C点的坐标是(0,2),
把(0,2)代入直线y=-x+m,
解得m=2,
∴解析式是y=-x+2,
令y=0,解得x=2,则A点的坐标是(2,0),
②在y=-
| ||
| 3 |

解得x=2
| 3 |
| 3 |
根据A、B、C的坐标得到OC=2,OA=2,OB=2
| 3 |
根据三角函数得到:tan∠CBO=
| CO |
| BO |
| ||
| 3 |
故∠ABC=30°.
如图1,连接AE,CE,过点E作EW⊥y轴于点W,ET⊥x轴于点T,
则∠AEC=60°,
∴△ACE是等边三角形,边长是2
| 2 |
∵∠WCE=180°-∠OCA-∠ECA=75°,
∠EAT=180°-∠CAO-∠EAC=75°,
∴∠WCE=∠EAT,
在△WCE和△TAE中,
|
∴△WCE≌△TAE,
∴WE=ET,
∵ET⊥AB,

∴AT=BT,
∵AB=OB-OA=2
| 3 |
∴AT=
| 3 |
∴OT=
| 3 |
| 3 |
因而E的坐标是(
| 3 |
| 3 |
故AE=
(
|
| 2 |
即半径是2
| 2 |
| 2 |

③如图2所示:MN为⊙E中任一弦,它对的圆周角为∠B,当AM为直径,
则∠ANM为直角,则sinB=sinA=
| MN |
| AM |
即MN=AM•sinA①(其实就是正弦定理),
根据点P在⊙E外,如图3,连接AN,
则∠MAN=∠ANC-∠P=∠ABC-∠P=30°-θ,
由①得:MN=4
| 2 |
点评:本题主要考查了圆的综合应用以及待定系数法求函数解析式,并且考查了三角函数的定义等知识,利用当AM为直径得出MN=AM•sinA继而得出答案是解题关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
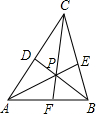 通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为
通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为 (2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC,
(2014•宝山区一模)通过锐角三角比的学习,我们已经知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长比与角的大小之间可以相互转化.类似的我们可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图在△ABC中,AB=AC, BAC的平分线,AD⊥BC于D.
BAC的平分线,AD⊥BC于D.
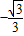 x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,
x+2相交于y轴上的点C,与x轴分别交于点A、B.经过A、B、C三点作⊙E,点P是第一象限内⊙E外的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,