��Ŀ����
��ͼ���ھ���ABCD�У�AB=6��AD= ����E��AD�����ȷֵ㣬��AE
����E��AD�����ȷֵ㣬��AE DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ
DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ ��
��

��1������Q���B�غ�ʱ����DP�ij��ȣ�
��2����AB���е�ΪN��PQ���߶�BE�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ�� Ϊ���������Σ������ڣ���ֱ��д��ʱ��
Ϊ���������Σ������ڣ���ֱ��д��ʱ�� ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3����� ���ı���
���ı��� ���ص����ֵ����ΪS������S��
���ص����ֵ����ΪS������S�� �ĺ�����ϵʽ����Ӧ���Ա���
�ĺ�����ϵʽ����Ӧ���Ա��� ��ȡֵ��Χ��
��ȡֵ��Χ��
 ����E��AD�����ȷֵ㣬��AE
����E��AD�����ȷֵ㣬��AE DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ
DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ ��
��
��1������Q���B�غ�ʱ����DP�ij��ȣ�
��2����AB���е�ΪN��PQ���߶�BE�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ��
 Ϊ���������Σ������ڣ���ֱ��д��ʱ��
Ϊ���������Σ������ڣ���ֱ��д��ʱ�� ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ���3�����
 ���ı���
���ı��� ���ص����ֵ����ΪS������S��
���ص����ֵ����ΪS������S�� �ĺ�����ϵʽ����Ӧ���Ա���
�ĺ�����ϵʽ����Ӧ���Ա��� ��ȡֵ��Χ��
��ȡֵ��Χ����1��3 ��2�� ��
��  ��
��  ��3��
��3��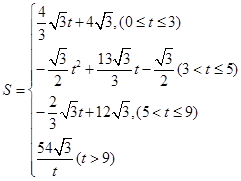
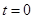 ��
��  ��
�� 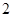 ��3��
��3��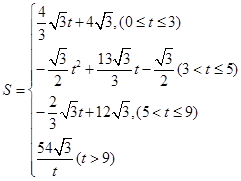
�����������������ͼ������������Уȴ�ֱ��AB��
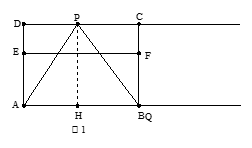
�ߡ�PQA=60�㣬AD=3
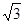 ��
����PH=3
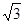 ��
����
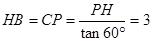 ��
����DP=DC��CP=6��3=3��
��2�����ڴ��ڵ�P��ʹ��
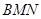 ����������
���������� ��
��  ��
��  ��
����3�����
 ���ı���
���ı��� ���ص����ֵ����ΪS
���ص����ֵ����ΪS ��Q��B���غϣ�P����CD�ߵ��е㴦����ʱ��
��Q��B���غϣ�P����CD�ߵ��е㴦����ʱ�� �ǵȱ������Σ��������ı���
�ǵȱ������Σ��������ı��� ���ص����ֵ����S=
���ص����ֵ����S=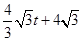 ����
����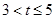 ʱ��
ʱ�� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=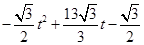 ����
����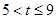 ����
���� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=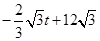 ����
����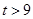 ����
���� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=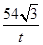 ������������
������������ ���ı���
���ı��� ���ص����ֵ����
���ص����ֵ����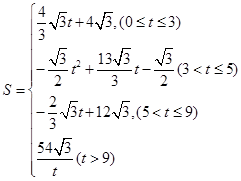
���������⿼�����Ǻ��������������Σ�������ϵʽ��Ҫ��ѧ���������Ǻ����Ķ��壬���������ε����ʣ��������Ľ���ʽ�����⿼����֪ʶ�㣬�ѶȽϴ�

��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ
 ��ͼ���ཻ��A(��2��1)��B(1��n)���㡣
��ͼ���ཻ��A(��2��1)��B(1��n)���㡣
 ��һ�κ���
��һ�κ��� �Ͷ��κ���
�Ͷ��κ��� .
.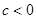 ʱ, ����
ʱ, ���� �����ֵ;
�����ֵ; ��ֵ.
��ֵ. ���֣���ʾ�ڹ�����������е�ʱ�䣬
���֣���ʾ�ڹ�����������е�ʱ�䣬 ���ף���ʾ�������е�·�̣�
���ף���ʾ�������е�·�̣�

 ��
�� ����ʾ��
����ʾ�� ��
�� ��ʵ�����壻
��ʵ�����壻 �֣��ס��������������ֿ����֦������÷ֱ�Ϊ
�֣��ס��������������ֿ����֦������÷ֱ�Ϊ Ԫ��
Ԫ�� Ԫ��
Ԫ��



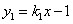 ��x�������ύ�ڵ�A��2��0������OAΪ����x���Ϸ���������OABC���ӳ�CB��ֱ��
��x�������ύ�ڵ�A��2��0������OAΪ����x���Ϸ���������OABC���ӳ�CB��ֱ�� �ڵ�D������BDΪ��������������BDEF��
�ڵ�D������BDΪ��������������BDEF��
 ����
���� ����x��ȡֵ��Χ��
����x��ȡֵ��Χ�� ������
������