题目内容
如图，△ABC是⊙O的内接三角形，⊙O的直径为8厘米，∠CBA=45°，求弦CA的长．分析：首先连接AO，CO，由∠CBA=45°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠AOC的度数，然后利用勾股定理，即可求得弦CA的长．
解答：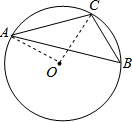
解：连接AO，CO．
∵∠CBA=45°，
∴∠COA=2∠CBA=90°，
∵⊙O的直径为8cm，
∴OA=OC=4cm，
在Rt△CAO中，CA=
=4
（cm）．
解：连接AO，CO．∵∠CBA=45°，
∴∠COA=2∠CBA=90°，
∵⊙O的直径为8cm，
∴OA=OC=4cm，
在Rt△CAO中，CA=
| OA2+OC2 |
| 2 |
点评：此题考查了圆周角定理与勾股定理．此题比较简单，准确作出辅助线，掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用是解此题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，△ABC是边长为2的等边三角形，将△ABC沿射线BC向右平移到△DCE，连接AD、BD，下列结论错误的是（ ）
如图，△ABC是锐角三角形，以BC为直径作⊙O，AD是⊙O的切线，从AB上一点E作AB的垂线交AC的延长线于F，若
（2013•玉林）如图，△ABC是⊙O内接正三角形，将△ABC绕点O顺时针旋转30°得到△DEF，DE分别交AB，AC于点M，N，DF交AC于点Q，则有以下结论：①∠DQN=30°；②△DNQ≌△ANM；③△DNQ的周长等于AC的长；④NQ=QC．其中正确的结论是
如图，△ABC是等边三角形，D是BC边的中点，点E在AC的延长线上，且∠CDE=30°．若AD=5，求DE的长．
如图，△ABC是等边三角形，则∠ABD=