题目内容

已知抛物线y=-ax²+2ax+b与x轴的一个交点为A（-1，0），与y轴的正半轴交于点C．
（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点B的坐标；
（2）当点C在以AB为直径的⊙P上时，求抛物线的解析式．

解：（1）根据抛物线的对称轴公式及抛物线的对称性可知，
对称轴为直线x=1，B（3，0）；

（2）连接BC，
∵AB为直径，
∴∠ACB=90°，
又CO⊥AB，
∴△AOC∽△COB，
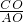∴ $\text{[math]}$ = $\text{[math]}$ ，即 $\text{[math]}$ = $\text{[math]}$
解得CO= $\text{[math]}$ ，即C（0， $\text{[math]}$ ）
设过A（-1，0），B（3，0）两点的抛物线解析式为y=a（x+1）（x-3）
将C（0， $\text{[math]}$ ）代入得-3a= $\text{[math]}$ ，a=- $\text{[math]}$
∴y=- $\text{[math]}$ （x+1）（x-3），
即y=- $\text{[math]}$ x²+ $\text{[math]}$ x+ $\text{[math]}$ ．
分析：（1）根据对称轴公式，对称轴x=- $\text{[math]}$ =1，根据抛物线的对称性，A（-1，0）、B两点关于对称轴的对称，可推出B点坐标；
（2）当点C在以AB为直径的⊙P上时，△ABC为直角三角形，已知OA=1，OB=3，由△AOC∽△COB，利用相似比可求OC，即C点坐标，设抛物线解析式的交点式，将C点坐标代入即可．
点评：本题考查了抛物线对称轴公式，抛物线对称性的运用，待定系数法求抛物线解析式的方法．综合运用了圆的对称性，直角三角形中的相似三角形的问题．