题目内容
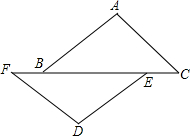 (2013•随州)如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
(2013•随州)如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.提供的三个条件是:①AB=DE;②AC=DF;③AC∥DF.
分析:由BF=CE可得EF=CB,再有条件∠ABC=∠DEF不能证明△ABC≌△DEF;可以加上条件①AB=DE,利用SAS定理可以判定△ABC≌△DEF.
解答:解:不能;
选择条件:①AB=DE;
∵BF=CE,
∴BF+BE=CE+BE,
即EF=CB,
在△ABC和△DFE中
,
∴△ABC≌△DFE(SAS).
选择条件:①AB=DE;
∵BF=CE,
∴BF+BE=CE+BE,
即EF=CB,
在△ABC和△DFE中
|
∴△ABC≌△DFE(SAS).
点评:此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
(2013•随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( ) (2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( ) (2013•随州)如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )
(2013•随州)如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( ) (2013•随州)如图是一圆锥,在它的三视图中,既是中心对称图形,又是轴对称图形的是它的
(2013•随州)如图是一圆锥,在它的三视图中,既是中心对称图形,又是轴对称图形的是它的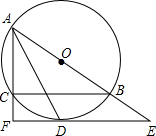 (2013•随州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.
(2013•随州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.