题目内容
如图,点E在正方形ABCD外,连接AE、BE、DE,过点A作AE的垂线交DE于点F.若AE=AF=1,BF= .则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为
.则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△AFD+S△AFB=1+
;③EB⊥ED;④S△AFD+S△AFB=1+ ;⑤S正方形ABCD =4+
;⑤S正方形ABCD =4+ .其中正确结论的序号是 ( )
.其中正确结论的序号是 ( )

 .则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为
.则下列结论:①△AFD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△AFD+S△AFB=1+
;③EB⊥ED;④S△AFD+S△AFB=1+ ;⑤S正方形ABCD =4+
;⑤S正方形ABCD =4+ .其中正确结论的序号是 ( )
.其中正确结论的序号是 ( )
| A.①③④ | B.①②⑤ | C.③④⑤ | D.①③⑤ |
A.
试题分析:在正方形ABCD中,AB=AD,
∵AP⊥AE,
∴∠BAE+∠BAP=90°,
又∵∠DAP+∠BAP=∠BAD=90°,
∴∠BAE=∠DAP,
在△APD和△AEB中,
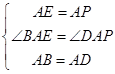 ,
,∴△APD≌△AEB(SAS),故①正确;
∵AE=AP,AP⊥AE,
∴△AEP是等腰直角三角形,
∴∠AEP=∠APE=45°,
∴∠AEB=∠APD=180°﹣45°=135°,
∴∠BEP=135°﹣45°=90°,
∴EB⊥ED,故③正确;
∵AE=AP=1,
∴PE=
 AE=
AE= ,
,在Rt△PBE中,BE=
 ,
,∴S△APD+S△APB=S△APE+S△BPE,
=
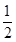 ×1×1+
×1×1+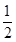 ×
× ×2,
×2,=0.5+
 ,故④正确;
,故④正确;过点B作BF⊥AE交AE的延长线于F,
∵∠BEF=180°﹣135°=45°,
∴△BEF是等腰直角三角形,
∴BF=
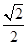 ×2=
×2= ,
,即点B到直线AE的距离为
 ,故②错误,
,故②错误,综上所述,正确的结论有①③④.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,如图1所示,将△
,如图1所示,将△ 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A(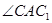 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。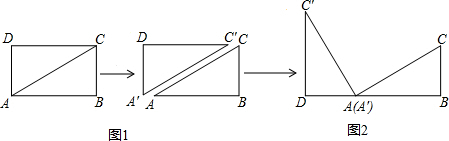

 ,求
,求 的度数。
的度数。
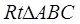 中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=4,BC=7,CD=2.
中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=4,BC=7,CD=2.