题目内容
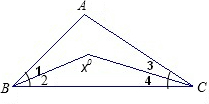
如图，在△ABC中，∠B=66°，∠C=54°，AD是∠BAC的平分线，DE平分∠ADC交于AC于点E，求∠BDE的大小．
∵∠B=66°，∠C=54°，
∴∠BAC=180°-66°-54°=60°．
∵AD是∠BAC的平分线，
∴∠BAD=30°，
∴∠ADB=180°-66°-30°=84°，
∴∠ADC=96°，
∵DE平分∠ADC，
∴∠BDE=84°+
×96°=132°．
∴∠BAC=180°-66°-54°=60°．
∵AD是∠BAC的平分线，
∴∠BAD=30°，
∴∠ADB=180°-66°-30°=84°，
∴∠ADC=96°，
∵DE平分∠ADC，
∴∠BDE=84°+
| 1 |
| 2 |
练习册系列答案
全能测控期末小状元系列答案
相关题目
