题目内容
4. 如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED等于70°.
如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED等于70°.
分析 在△BCO中利用外角和定理求得∠DBE的度数,然后证明△ADO≌△BCO,求得∠D的度数,在△BED中利用内角和定理求解.
解答 解:∠DBE=∠O+∠C=60°+25°=85°,
∵在△ADO和△BCO,
$\left\{\begin{array}{l}{OA=OB}\\{∠O=∠O}\\{OC=OD}\end{array}\right.$,
∴△ADO≌△BCO,
∴∠D=∠C=25°,
∴∠BED=180°-∠D-∠DBE=180°-25°-85°=70°.
故答案是:70°.
点评 本题考查全等三角形的判定与性质,以及三角形的外角的性质以及三角形内角和定理,正确证明△ADO≌△BCO是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
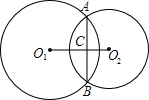 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为17cm和10cm,公共弦AB=16cm,求O1O2的长.
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为17cm和10cm,公共弦AB=16cm,求O1O2的长. 如图,将一根25cm长的细木棒放入长、宽、高的平方分别为64cm2、36cm2和300cm2的长方体无盖盒子中,则细木棒露在盒外面的最短长度是5cm.
如图,将一根25cm长的细木棒放入长、宽、高的平方分别为64cm2、36cm2和300cm2的长方体无盖盒子中,则细木棒露在盒外面的最短长度是5cm. 如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)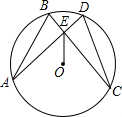 如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.
如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.