题目内容
 如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c-k=0有两个不相等的实数根,则k的取值范围是
如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c-k=0有两个不相等的实数根,则k的取值范围是
- A.k<3
- B.k>3
- C.k≤3
- D.k≥3
A
分析:先根据抛物线的图象可知a<0,其最大值为3,故 =3,再根据关于x的方程ax2+bx+c-k=0有两个不相等的实数根可知△>0,进而可求出k的取值范围.
=3,再根据关于x的方程ax2+bx+c-k=0有两个不相等的实数根可知△>0,进而可求出k的取值范围.
解答:∵抛物线开口向下,
∴a<0,
∵抛物线顶点的纵坐标为3,
∴ =3,即4ac-b2=12a①,
=3,即4ac-b2=12a①,
∵关于x的方程ax2+bx+c-k=0有两个不相等的实数根,
∴△=b2-4a(c-k)>0,即b2-4ac+4ak>0②,把①代入②得,-12a+4ak>0,
∴-3+k<0,即k<3.
故选A.
点评:本题考查的是抛物线与x轴的交点及一元二次方程的判别式、不等式的基本性质,熟知以上知识是解答此题的关键.
分析:先根据抛物线的图象可知a<0,其最大值为3,故
 =3,再根据关于x的方程ax2+bx+c-k=0有两个不相等的实数根可知△>0,进而可求出k的取值范围.
=3,再根据关于x的方程ax2+bx+c-k=0有两个不相等的实数根可知△>0,进而可求出k的取值范围.解答:∵抛物线开口向下,
∴a<0,
∵抛物线顶点的纵坐标为3,
∴
 =3,即4ac-b2=12a①,
=3,即4ac-b2=12a①,∵关于x的方程ax2+bx+c-k=0有两个不相等的实数根,
∴△=b2-4a(c-k)>0,即b2-4ac+4ak>0②,把①代入②得,-12a+4ak>0,
∴-3+k<0,即k<3.
故选A.
点评:本题考查的是抛物线与x轴的交点及一元二次方程的判别式、不等式的基本性质,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
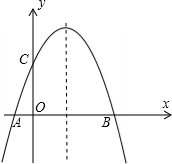 如图,是二次函数y=ax2+bx+c的图象,则下列说法错误的是( )
如图,是二次函数y=ax2+bx+c的图象,则下列说法错误的是( )| A、a<0 | ||
B、对称轴是直线x=-
| ||
| C、ab<0 | ||
D、x>-
|
 6、如图,是二次函数y=ax2+bx+c的图象,点P(a+b,ac)是平面直角坐标系内的点,则点P在( )
6、如图,是二次函数y=ax2+bx+c的图象,点P(a+b,ac)是平面直角坐标系内的点,则点P在( ) 下列说法正确的是
下列说法正确的是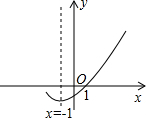 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分, 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则方程ax2+bx+c=0的两根分别为
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,则方程ax2+bx+c=0的两根分别为