题目内容
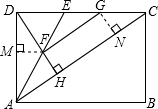
在矩形ABCD中,AE平分∠DAC,DH⊥AC于H交AE于点F,过F作FG∥AC交CD于点G,
(1)求证:DE=CG;
(2)若AC平分∠BAE,FH=2,求四边形ECHF的面积.
(1)求证:DE=CG;
(2)若AC平分∠BAE,FH=2,求四边形ECHF的面积.
考点:矩形的性质,全等三角形的判定与性质
专题:
分析:(1)根据角平分线的定义可得∠DAE=∠CAE,然后根据等角的余角相等求出∠DEF=∠DFE,再根据等角对等边的性质求出DE=DF,过点F作FM⊥AD于M,过点G作GN⊥AC于N,根据角平分线上的点到角的两边距离相等可得FH=FM,根据矩形的对边相等求出FH=GN,再求出∠GCN=∠FDA,然后利用“角角边”证明△DMF和△CNH全等,根据全等三角形对应边相等可得CG=DF,从而得证;
(2)求出∠DAE=∠CAE=∠BAC=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AF,再求出AH、AM,然后求出AD、CD,解直角三角形求出DE,再求出CE,最后根据S四边形ECHF=S△ACE-S△AFH列式计算即可得解.
(2)求出∠DAE=∠CAE=∠BAC=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AF,再求出AH、AM,然后求出AD、CD,解直角三角形求出DE,再求出CE,最后根据S四边形ECHF=S△ACE-S△AFH列式计算即可得解.
解答:(1)证明:∵AE平分∠DAC,
∴∠DAE=∠CAE,
∵∠DEF+∠DAE=∠AFH+∠CAE,∠AFH=∠DFE,
∴∠DEF=∠DFE,
∴DE=DF,
 过点F作FM⊥AD于M,过点G作GN⊥AC于N,
过点F作FM⊥AD于M,过点G作GN⊥AC于N,
∵AE平分∠DAC,
∴FH=FM,
∵DH⊥AC,FG∥AC,
∴四边形FHNG是矩形,
∴FH=GN,
∴FM=GN,
∵DH⊥AC,
∴∠GCN+∠CDH=90°,
∵∠FDA+∠CDH=∠ADC=90°,
∴∠GCN=∠FDA,
在△DMF和△CNH中,
,
∴△DMF≌△CNH(AAS),
∴CG=DF,
∴DE=CG;
(2)解:∵AC平分∠BAE,AE平分∠DAC,
∴∠DAE=∠CAE=∠BAC=90°÷3=30°,
∵FH=2,
∴AF=2FH=2×2=4,
∴AM=AH=
=2
,
∵∠ADF=∠ACD=∠BAC=30°,FM⊥AD,
∴AD=2AM=2×2
=4
,
∴CD=
AD=
×4
=12,
∵DE=
×4
=4,
∴CE=CD-DE=12-4=8,
∴S四边形ECHF=S△ACE-S△AFH
=
×8×4
-
×2×2
=16
-2
=14
.
∴∠DAE=∠CAE,
∵∠DEF+∠DAE=∠AFH+∠CAE,∠AFH=∠DFE,
∴∠DEF=∠DFE,
∴DE=DF,
 过点F作FM⊥AD于M,过点G作GN⊥AC于N,
过点F作FM⊥AD于M,过点G作GN⊥AC于N,∵AE平分∠DAC,
∴FH=FM,
∵DH⊥AC,FG∥AC,
∴四边形FHNG是矩形,
∴FH=GN,
∴FM=GN,
∵DH⊥AC,
∴∠GCN+∠CDH=90°,
∵∠FDA+∠CDH=∠ADC=90°,
∴∠GCN=∠FDA,
在△DMF和△CNH中,
|
∴△DMF≌△CNH(AAS),
∴CG=DF,
∴DE=CG;
(2)解:∵AC平分∠BAE,AE平分∠DAC,
∴∠DAE=∠CAE=∠BAC=90°÷3=30°,
∵FH=2,
∴AF=2FH=2×2=4,
∴AM=AH=
| 42-22 |
| 3 |
∵∠ADF=∠ACD=∠BAC=30°,FM⊥AD,
∴AD=2AM=2×2
| 3 |
| 3 |
∴CD=
| 3 |
| 3 |
| 3 |
∵DE=
| ||
| 3 |
| 3 |
∴CE=CD-DE=12-4=8,
∴S四边形ECHF=S△ACE-S△AFH
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
=16
| 3 |
| 3 |
=14
| 3 |
点评:本题考查了矩形的性质,全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,等角的余角相等的性质,解直角三角形,难点在于作辅助线构造出矩形和全等三角形.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
观察下列球的排列规律(其中●是实心球, 是空心球):
是空心球):
从第一个球起到第2013个球止,共有实心球( )个.
 是空心球):
是空心球):
从第一个球起到第2013个球止,共有实心球( )个.
| A、201 | B、202 |
| C、604 | D、603 |
 已知:如图,AD垂直平分BE,且AB+BD=DC,求证:点E在线段AC的垂直平分线上.
已知:如图,AD垂直平分BE,且AB+BD=DC,求证:点E在线段AC的垂直平分线上. 如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?.
如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿那个方向航行吗?.