Question

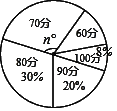
【题目】某班共50名同学，统一参加区教育局举办的防“雾霾”知识检验，成绩分别记作60分、70分、80分、90分、100分，现统计出80分、90分、100分的人数，制成不完整的扇形统计图．

（1）若n=108，则60分的人数为 ；

（2）若从这50份试卷中，随机抽取一份，求抽到试卷的分数低于80分的概率；

（3）若成绩的唯一众数为80分，求这个班平均成绩的最大值．

Answer 1

【答案】(1) 6人；(2) (3) 78

【解析】(1)、根据n的值得出70分所占的百分比，从而得出60分所占的百分比，从而得出人数；(2)、首先求出低于80分的人数，然后根据概率的计算法则得出答案；(3)、根据题意可得80分的人数为15人，根据80为唯一的众数可知70分的人数为14人时，这个班的平均数最大，从而根据平均数的求法得出答案．

(1)、若n=108， 则×100%=30%，

∴60分的学生所占比例为：1﹣30%﹣30%﹣20%﹣8%=12%，则60分的人数为：12%×50=6（人）；

(2)、低于80分的人数为：50×（12%+30%）=21（人），

则从这50份试卷中，随机抽取一份，求抽到试卷的分数低于80分的概率为：；

(3)、∵80分的人数为：50×30%=15（人），且80分为成绩的唯一众数，所以当70分的人数为14人时，这个班的平均数最大，

∴最大值为：（50×8%×100+50×20%×90+50×30%×80+14×70+7×60）÷50=78（分）．