题目内容
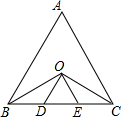 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.(1)求证:△DOE是等边三角形;
(2)线段BD,DE,EC三者存什么数量关系?写出你的判断过程;
(3)数学学习不仅要能解决问题,还要善于提出问题,结合本题,在现有图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不要解答)
(1)证明:
(2)我的判断是:
证明如下:
(3)我提出的问题是:
①
②
考点:等边三角形的判定与性质
专题:
分析:(1)证明∠ODE=∠OED,即可解决问题.
(2)证明OD=DE=OE;证明BD=OD;同理可证OE=EC,即可解决问题.
(3)观察图形,借助(1)、(2)中的结论,可以发现△OBE、△ODE均为直角三角形,且BE=2OE.
(2)证明OD=DE=OE;证明BD=OD;同理可证OE=EC,即可解决问题.
(3)观察图形,借助(1)、(2)中的结论,可以发现△OBE、△ODE均为直角三角形,且BE=2OE.
解答: 解:(1)∵△ABC是等边三角形,且OD∥AB,OE∥AC,
解:(1)∵△ABC是等边三角形,且OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴∠ODE=∠OED=60°,
∴△ODE是等边三角形.
(2)BD=DE=EC;理由如下:
∵△ODE是等边三角形,
∴OD=DE=OE;
∵∠ABC与∠ACB的平分线相交于点O,且OD∥AB,
∴∠ABO=∠DBO,∠ABO=∠DOB,
∴∠DBO=∠DOB,
∴BD=OD;同理可证:OE=EC,
∴BD=DE=EC.
(3)①△OBE、△OCD均为直角三角形;
②BE=2OE.
 解:(1)∵△ABC是等边三角形,且OD∥AB,OE∥AC,
解:(1)∵△ABC是等边三角形,且OD∥AB,OE∥AC,∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴∠ODE=∠OED=60°,
∴△ODE是等边三角形.
(2)BD=DE=EC;理由如下:
∵△ODE是等边三角形,
∴OD=DE=OE;
∵∠ABC与∠ACB的平分线相交于点O,且OD∥AB,
∴∠ABO=∠DBO,∠ABO=∠DOB,
∴∠DBO=∠DOB,
∴BD=OD;同理可证:OE=EC,
∴BD=DE=EC.
(3)①△OBE、△OCD均为直角三角形;
②BE=2OE.
点评:该题主要考查了等边三角形的判定及其性质的应用问题;牢固掌握等边三角形的性质是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
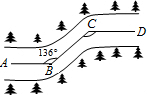 一条公路两次转弯后又回到原来的方向(即AB∥CD,如图)如果第一次转弯时∠B=136°,那么∠C应是( )
一条公路两次转弯后又回到原来的方向(即AB∥CD,如图)如果第一次转弯时∠B=136°,那么∠C应是( )| A、136° | B、124° |
| C、144° | D、154° |
在平面直角坐标系中,点(-5,2)所在的象限为( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
| A、极差是15 |
| B、众数是88 |
| C、中位数是86 |
| D、平均数是87 |
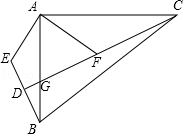 如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D.
如图,在△ABC中,∠BAC=90°,∠EAF=90°,AB•AF=AC•AE.连接CF并延长CF交AB于点G,交BE于点D.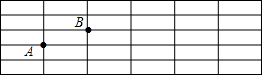 如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( )
如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( )