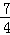题目内容
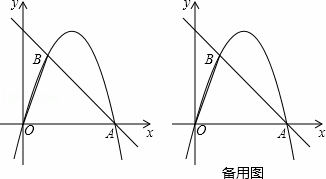
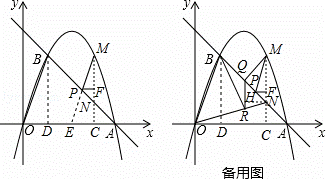
如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR∥MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
解:(1)∵y=﹣x+4与x轴交于点A,
∴A(4,0),
∵点B的横坐标为1,且直线y=﹣x+4经过点B,
∴B(1,3),
∵抛物线y=ax2+bx经过A(4,0),B(1,3),
∴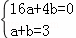 ,
,
解得: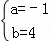 ,
,
∴a=﹣1,b=4;
(2)如图,作BD⊥x轴于点D,延长MP交x轴于点E,
∵B(1,3),A(4,0),
∴OD=1,BD=3,OA=4,
∴AD=3,
∴AD=BD,
∵∠BDA=90°,∠BAD=∠ABD=45°,
∵MC⊥x轴,∴∠ANC=∠BAD=45°,
∴∠PNF=∠ANC=45°,
∵PF⊥MC,∴∠FPN=∠PNF=45°,
∴NF=PF=t,
∵∠DFM=∠ECM=90°,∴PF∥EC,
∴∠MPF=∠MEC,
∵ME∥OB,∴∠MEC=∠BOD,
∴∠MPF=∠BOD,
∴tan∠BOD=tan∠MPF,
∴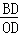 =
=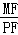 =3,
=3,
∴MF=3PF=3t,
∵MN=MF+FN,
∴d=3t+t=4t;
(3)如备用图,由(2)知,PF=t,MN=4t,
∴S△PMN=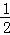 MN×PF=
MN×PF=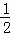 ×4t×t=2t2,
×4t×t=2t2,
∵∠CAN=∠ANC,
∴CN=AC,
∴S△ACN=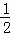 AC2,
AC2,
∵S△ACN=S△PMN,
∴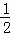 AC2=2t2,
AC2=2t2,
∴AC=2t,∴CN=2t,
∴MC=MN+CN=6t,
∴OC=OA﹣AC=4﹣2t,
∴M(4﹣2t,6t),
由(1)知抛物线的解析式为:y=﹣x2+4x,
将M(4﹣2t,6t)代入y=﹣x2+4x得:
﹣(4﹣2t)2+4(4﹣2t)=6t,
解得:t1=0(舍),t2=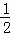 ,
,
∴PF=NF=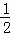 ,AC=CN=1,OC=3,MF=
,AC=CN=1,OC=3,MF=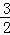 ,PN=
,PN=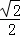 ,PM=
,PM=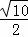 ,AN=
,AN=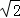 ,
,
∵AB=3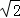 ,
,
∴BN=2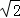 ,
,
作NH⊥RQ于点H,
∵QR∥MN,
∴∠MNH=∠RHN=90°,
∠RQN=∠QNM=45°,∴∠MNH=∠NCO,
∴NH∥OC,
∴∠HNR=∠NOC,
∴tan∠HNR=tan∠NOC,
∴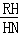 =
=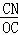 =
=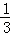 ,
,
设RH=n,则HN=3n,
∴RN=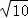 n,QN=3
n,QN=3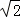 n,
n,
∴PQ=QN﹣PN=3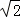 n﹣
n﹣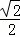 ,
,
∵ON=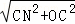 =
=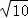 ,
,
OB=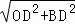 =
=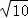 ,
,
∴OB=ON,∴∠OBN=∠BNO,
∵PM∥OB,
∴∠OBN=∠MPB,
∴∠MPB=∠BNO,
∵∠MQR﹣∠BRN=45°,∠MQR=∠MQP+∠RQN=∠MQP+45°,
∴∠BRN=∠MQP,
∴△PMQ∽△NBR,
∴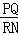 =
=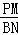 ,
,
∴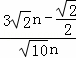 =
=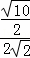 ,
,
解得:n=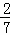 ,
,
∴R的横坐标为:3﹣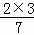 =
=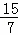 ,R的纵坐标为:1﹣
,R的纵坐标为:1﹣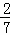 =
=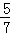 ,
,
∴R(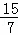 ,
,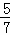 ).
).

对参加某次野外训练的中学生的年龄(单位:岁)进行统计,结果如表:
| 年龄 | 13 | 14 | 15 | 16 | 17 | 18 |
| 人数 | 4 | 5 | 6 | 6 | 7 | 2 |
则这些学生年龄的众数和中位数分别是( )
|
| A. | 17,15.5 | B. | 17,16 | C. | 15,15.5 | D. | 16,16 |
为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
|
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) |
| 甲型挖掘机 | 100 | 60 |
| 乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
已知一组数据:1,2,6,3,3,下列说法正确的是( )
|
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是4 | D. | 方差是5 |
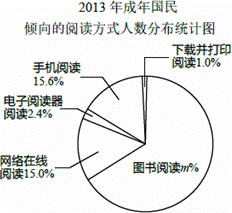
根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
| 2009~2013年成年国民 年人均阅读图书数量统计表 | |
| 年份 | 年人均阅读图书数量(本) |
| 2009 | 3.88 |
| 2010 | 4.12 |
| 2011 | 4.35 |
| 2012 | 4.56 |
| 2013 | 4.78 |
根据以上信息解答下列问题:
(1)直接写出扇形统计图中m的值;
(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为 5 本;
(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为 7500 本.
 有意义,则x的取值范围是( )
有意义,则x的取值范围是( ) B. x≤
B. x≤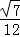 B.
B. 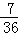
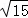 C.
C. 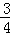
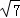 D.
D.