题目内容
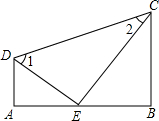 如图,CB⊥AB,∠1+∠2=90°,DE、CE分别平分∠ADC、∠BCD,求证:AB⊥DA.
如图,CB⊥AB,∠1+∠2=90°,DE、CE分别平分∠ADC、∠BCD,求证:AB⊥DA.分析:根据角平分线的定义可得∠ADC=2∠1,∠BCD=2∠2,然后求出∠ADC+∠BCD=180°,根据同旁内角互补,两直线平行可得AD∥BC,再根据两直线平行,同旁内角互补证明即可.
解答:证明:∵DE、CE分别平分∠ADC、∠BCD,
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,
∴∠ADC+∠BCD=2×90°=180°,
∴AD∥BC,
又∵CB⊥AB,
∴∠B=90°,
∴∠A=180°-90°=90°,
∴AB⊥DA.
∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,
∴∠ADC+∠BCD=2×90°=180°,
∴AD∥BC,
又∵CB⊥AB,
∴∠B=90°,
∴∠A=180°-90°=90°,
∴AB⊥DA.
点评:本题考查了角平分线的定义,平行线的判定与性质,以及垂直的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.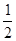 AB,AC=
AB,AC=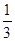 AD,AB=
AD,AB=
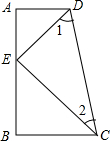 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.