Question

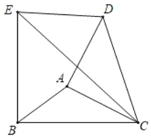
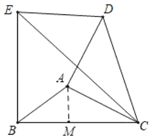
【题目】如图，分别以△ABC中BC和AC为腰向外作等腰直角△EBC和等腰直角△DAC，连结DE，且DE∥BC，EB＝BC＝6，四边形EBCD的面积为24，则AB的长为_____．

Answer 1

【答案】

【解析】

由题意可得S△DEC=24-18=6，由等腰三角形的性质可得BE=BC=6，AC=DA，∠EBC=∠DAC=90°，∠ECB=45°=∠DCA，可证△ABC∽△DEC，由相似三角形的性质可得S△ABC=3，∠DEC=∠ABC=45°，由三角形的面积公式可求AB的长．

解：∵S△BEC＝BC×BE＝18，四边形EBCD的面积为24，

∴S△DEC＝24﹣18＝6

∵△EBC与△DAC是等腰直角三角形

∴BE＝BC＝6，AC＝DA，∠EBC＝∠DAC＝90°，∠ECB＝45°＝∠DCA，

∴EC＝BC，DC＝AC，∠BCA＝∠DCE，

∵，且∠BCA＝∠DCE，

∴△ABC∽△DEC

∴∠DEC＝∠ABC，

∴S△ABC＝＝3

∵DE∥BC

∴∠DEC＝∠ECB＝45°

∴∠ABC＝45°

如图，过点A作AM⊥BC于M

∵S△ABC＝×BC×AM＝3

∴AM＝1

∵∠ABC＝45°，AM⊥BC

∴∠ABC＝∠BAM＝45°

∴BM＝AM＝1，

∴AB＝

故答案为：.