Question

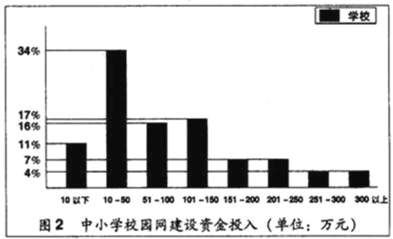
【题目】如图，在Rt△OAB中，∠AOB＝90°，OA＝OB＝4，以点O为圆心、2为半径画圆，点C是⊙O上任意一点，连接BC，OC．将OC绕点O按顺时针方向旋转90°，交⊙O于点D，连接AD．

（1）当AD与⊙O相切时，

①求证：BC是⊙O的切线；

②求点C到OB的距离．

（2）连接BD，CD，当△BCD的面积最大时，点B到CD的距离为　 　．

Answer 1

【答案】（1）①证明见解析；②点C到OB的距离是．（2）4+.

【解析】

（1）①先证明△BOC≌△AOD，则∠BCO=∠ADO=90°，BC是⊙O的切线；

②过点C作CE⊥OB，根据勾股定理得BC=2，由△BCO的面积公式可得OBCE=BCOC，求得CE=；

（2）当点C在⊙O上运动到△BCD是等腰三角形，且BO的延长线与CD垂直位置时，△BCD的面积最大（如图2），由等腰直角三角形的性质可求得OF=，则点B到CD的距离为4+．

（1）①证明：∵AD与⊙O相切，

∴∠ADO＝90°，

∵∠AOB＝∠COD＝90°，

∴∠AOB﹣∠AOC＝∠COD﹣∠AOC，即∠COB＝∠AOD，

∵OB＝OA，OC＝OD，

∴△BOC≌△AOD（SAS）．

∴∠BCO＝∠ADO＝90°．

∴BC是⊙O的切线；

②如图：

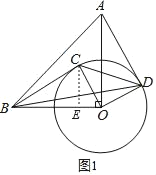
过点C作CE⊥OB，垂足为E，则CE即为点C到OB的距离，

在Rt△BOC中，∵OB＝4，OC＝2，

∴BC=，

∴OBCE＝BCOC，即4CE＝2×2，CE＝．

∴点C到OB的距离是；

（2）当点C在⊙O上运动到△BCD是等腰三角形，且BO的延长线与CD垂直位置时，

△BCD的面积最大（如图2），

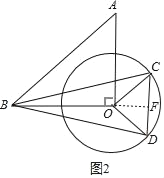
此时OB＝4，OC＝OD＝2，

∵△COD是等腰直角三角形，

∴，

∴．

故答案为：4+．