��Ŀ����
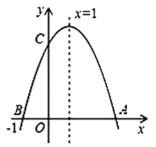
����Ŀ����ͼ1��ʾ��ֱ��y=x+c��x�ύ��A����4��0������y�ύ�ڵ�C��������y=��x2+bx+c����A��C��
��1���������ߵĽ���ʽ ;
��2����E�������ߵĶԳ����ϣ���CE+OE����Сֵ��
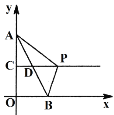
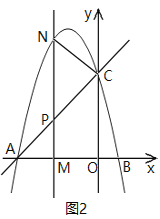
��3����ͼ2��ʾ��M���߶�OA����һ�����㣬����M��ֱ��x���ֱ����ֱ��AC�������߷ֱ��ڵ�P��N
������C��P��NΪ���������������APM���ƣ�����CPN�����Ϊ________��
������Pǡ�����߶�MN���е㣬��F��ֱ��AC��һ�����㣬������ƽ�����Ƿ���ڵ�D��ʹ�Ե�D��F��P��MΪ������ı��������Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵�����ɣ�
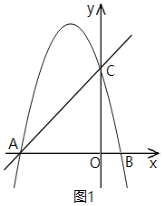
���𰸡���1��y=��x2��3x+4;��2��CE+OE����СֵΪ5;��3����![]() ��4;�ڴ��ڣ���PF=FMʱ����D��MN��ֱƽ�����ϣ���D��
��4;�ڴ��ڣ���PF=FMʱ����D��MN��ֱƽ�����ϣ���D��![]() ������PM=PFʱ�����������ʵ�D����Ϊ����1+
������PM=PFʱ�����������ʵ�D����Ϊ����1+ ![]() ��
�� ![]() ������1��
������1�� ![]() ����
���� ![]() ��,��MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��
��,��MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��
��������
��1������֪������������ʽ��
��2��ȡ��C���������ߵĶԳ���ֱ��l�ĶԳƵ�C����������֮���߶���̣���Сֵ�ɵã�
��3��������֪��ע�����������εķ������ۣ�
�����M���꣬���P���꣮ע���������ɵ����������Եױ�����ֱ��Ϊ�Գ���ԳƵõ��ģ����⼴Ϊ�о���CPNΪ���������ε������
��1����A����4��0������y=x+c
��c=4
��A����4��0����c=4����y=��x2+bx+c
��b=��3
�������߽���ʽΪy=��x2��3x+4
��2������C���������ߵĶԳ���ֱ��l�ĶԳƵ�C������OC������ֱ��l�ڵ�E����CE����ʱCE+OE��ֵ��С��

�������߶Գ���λ����x=��![]()
��CC��=3
�ɹ��ɶ���OC��=5
��CE+OE����СֵΪ5
��3���ٵ���CNP�ס�AMPʱ��

��CNP=90������NC���������߶Գ���Գ�
��NC=NP=3���CPN�����Ϊ![]()
����CNP�ס�MAPʱ

����֪��NCPΪ����ֱ�������Σ���NCP=90��
����C��CE��MN�ڵ�E�����M����Ϊ��a��0��
��EP=EC=��a��
��N��a����a2��3a+4����MP=��a2��3a+4������2a��=��a2��a+4
��P��a����a2��a+4��
����y=x+4
���a=��2
���CPN�����Ϊ4
�ڴ���
��M������a��0��
��N��a����a2��3a+4��
��P��������a��![]() ��
��
�ѵ�P�������y=��x+4
���a1=��4����ȥ����a=��1
��PF=FMʱ����D��MN��ֱƽ�����ϣ���D�� ![]() ��
��
��PM=PFʱ�����������ʵ�D����Ϊ����1+ ![]() ��
�� ![]() ������1��
������1�� ![]() ����
���� ![]() ��
��
��MP=MFʱ��M��D����ֱ��y=��x+4�Գƣ���D����Ϊ����4��3��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�����Ŀ�����գ�ȫʡ�����е�2019����б�ҵ��ѧ�������Թ���������ijʡ�������ľ���Ҫ�����������ɵĽ��е��У�ij��ѧ����ʽ����ǰ��Ϊ����ͬѧ�����������������л������ɼ���ͬʱΪ���˽�ѧ���ĵ�ǰˮƽ�������ν�����ģ�⿼�ԣ��������ȡ������ѧ���ʾ����飬�ֽ����������Ƴ����²�������ͳ��ͼ����
��� | �ɼ���Χx���֣� | Ƶ���������� |
A | 60��x��70 | 54 |
B | 50��x��60 | m |
C | 40��x��50 | n |
D | 30��x��40 | 6 |
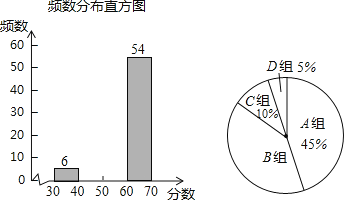
��1����ε�������������� ���ˣ����е�m���� ����n���� ����
��2������ͳ��ͼ��B���Ӧ��Բ�Ľ�Ϊ�� ���㣻
��3���벹ȫƵ���ֲ�ֱ��ͼ��
��4������У���꼶����ѧ��2700�����Ҷ��μ�����ʽ�ij��б�ҵ��ѧ�������ԣ�С��Ҳ�μ�����ο��Բ�����67�֣����涨60������Ϊ���㣬������ʦ��Ҫ�ڻ�������ѧ����������1������Ϊѧ��������ѧ��ѧ���Ǵ��ھ��飬��鵽С���ĸ��ʣ�