题目内容
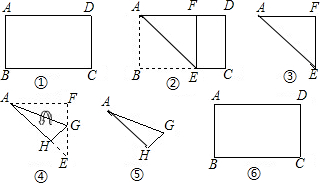
矩形纸片ABCD中,AD=12cm,现将这张纸片按下列图示方式折叠,AE是折痕.(1)如图1,P,Q分别为AD,BC的中点,点D的对应点F在PQ上,求PF和AE的长;
(2)如图2,
 ,点D的对应点F在PQ上,求AE的长;
,点D的对应点F在PQ上,求AE的长;(3)如图3,
 ,点D的对应点F在PQ上.
,点D的对应点F在PQ上.①直接写出AE的长(用含n的代数式表示); ②当n越来越大时,AE的长越来越接近于______.

【答案】分析:(1)根据P、Q是矩形ABCD中AD,BC的中点,可得 ,从而可得∠AFP=30°,∠FAD=60°然后利用三角函数值即可求解.
,从而可得∠AFP=30°,∠FAD=60°然后利用三角函数值即可求解.
(2)根据 ,求得FP,利用DE=EF,∠AED=∠AEF,∠AED=∠FGE,求证EF=GF,设DE=x,则GF=x利用△APG∽△ADE的对应边成比例可求的AE.
,求得FP,利用DE=EF,∠AED=∠AEF,∠AED=∠FGE,求证EF=GF,设DE=x,则GF=x利用△APG∽△ADE的对应边成比例可求的AE.
(3)①可得 ,②当n越来越大时,根据
,②当n越来越大时,根据 可判定AE的长.
可判定AE的长.
解答:解:(1)∵P、Q是矩形ABCD中AD,BC的中点,
∴ ,
,
∴∠AFP=30°,
∴ ,
,
∴∠FAD=60°,
∴ ,
,
∴ ,
,
(2)∵ ,
,
∴
∴ ,
,
∵DE=EF,∠AED=∠AEF,∠AED=∠FGE,
∴∠FGE=∠FEG,
∴EF=GF,
设DE=x,则GF=x
∵△APG∽△ADE,
∴ ,
,
∴
∴ ,
,
∴ ,
,
∴ ;
;
(3)①可得 ,
,
②∵ ,
,
∴当n越来越大时,AE越来越接近于12.
故答案为:12.

点评:此题涉及到相似三角形的判定与性质,矩形的性质,翻折变换(折叠问题)等知识点,综合性较强,特别是翻折变换(折叠问题)要求学生应具备一定的空间想象能力,因此此题有一定的拔高难度,属于难题.
 ,从而可得∠AFP=30°,∠FAD=60°然后利用三角函数值即可求解.
,从而可得∠AFP=30°,∠FAD=60°然后利用三角函数值即可求解.(2)根据
 ,求得FP,利用DE=EF,∠AED=∠AEF,∠AED=∠FGE,求证EF=GF,设DE=x,则GF=x利用△APG∽△ADE的对应边成比例可求的AE.
,求得FP,利用DE=EF,∠AED=∠AEF,∠AED=∠FGE,求证EF=GF,设DE=x,则GF=x利用△APG∽△ADE的对应边成比例可求的AE.(3)①可得
 ,②当n越来越大时,根据
,②当n越来越大时,根据 可判定AE的长.
可判定AE的长.解答:解:(1)∵P、Q是矩形ABCD中AD,BC的中点,
∴
 ,
,∴∠AFP=30°,
∴
 ,
,∴∠FAD=60°,
∴
 ,
,∴
 ,
,(2)∵
 ,
,∴

∴
 ,
,∵DE=EF,∠AED=∠AEF,∠AED=∠FGE,
∴∠FGE=∠FEG,
∴EF=GF,
设DE=x,则GF=x
∵△APG∽△ADE,
∴
 ,
,∴

∴
 ,
,∴
 ,
,∴
 ;
;(3)①可得
 ,
,②∵
 ,
,∴当n越来越大时,AE越来越接近于12.
故答案为:12.

点评:此题涉及到相似三角形的判定与性质,矩形的性质,翻折变换(折叠问题)等知识点,综合性较强,特别是翻折变换(折叠问题)要求学生应具备一定的空间想象能力,因此此题有一定的拔高难度,属于难题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
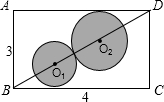 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )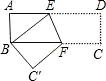 如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为
如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为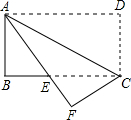 如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.
如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.