Question

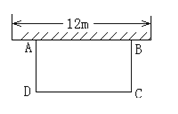
【题目】如图，科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD，其中一边AB靠墙，墙长为12m，设AD的长为m，DC的长为m。

（1）求与之间的函数关系式；

（2）根据实际情况，对于（1）式中的函数自变量能否取值为4m，若能，求出的值，若不能，请说明理由；

（3）若围成矩形科技园ABCD的三边材料总长不超过26m，材料AD和DC的长都是整米数，求出满足条件的所有围建方案。

Answer 1

【答案】(1) ;(2)不能，理由见解析;(3) AD＝5m，DC＝12m或AD＝6m，DC＝10m或AD＝10m，DC＝6m．

【解析】

（1）根据面积为60m2，可得出y与x之间的函数关系式；

（2）把x=4代入解析式得到y=15＞12，故x不能取4.

（3）由（1）的关系式，结合x、y都是正整数，可得出x的可能值，再由三边材料总长不超过26m，DC的长＜12，可得出x、y的值，继而得出可行的方案．

解：（1）由题意得，S矩形ABCD＝AD×DC＝xy，

故（x≥5）

（2）把x=4代入解析式=15＞12，故x不能取4.

（3）由，且x、y都是正整数，

可得x可取1，2，3，4，5，6，10，12，15，20，30，60，

∵2x＋y≤26，0＜y≤12，

∴符合条件的围建方案为：AD＝5m，DC＝12m或AD＝6m，DC＝10m或AD＝10m，DC＝6m．