题目内容
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式:
当 ,y= ;当
,y= ;当 时,y= ;
时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
(1) 1)50,2.5; (2)当0≤t≤20时,y=90-2.5t , 当20<t≤40时, y=2.5t-50 .(3)画图见解析;(4)5,40.
解析试题分析:(1)由于甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程,又因为y表示船离开池边B1B2的距离,所以图2中当t=0时对应的y值即为赛道的长度;因为30秒钟甲船从A1处运动到B1处,即20s运动50m,根据速度=路程÷时间,即可求出甲的速度;
(2)先根据图象的形状,可判断出甲船在0≤t≤30和30<t≤60时,y都是t的一次函数,设出其解析式,再运用待定系数法求解;
(3)乙的速度为2m/s,由B2到达A2的路程为赛道的长度50m,根据时间=路程÷速度,即可求出乙船由B2到达A2的时间为25s;乙船在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,起点在原点,据此在图2中画出乙船在2分钟内的函数图象;
(4)两个图象的交点个数即为相遇次数.
(1)50,2.5;
(2)当0≤t≤20时,y=90-2.5t , 当20<t≤40时, y=2.5t-50 .
(3)因为赛道的长度为50米,乙的速度为2米/秒,所以乙船由B2到达A2的时间为25秒; 乙在3分钟内的函数图象如图5所示: 
(4)从上图可知甲、乙共相遇5次.40米
考点: 一次函数的应用.

九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.

 (元)与采购量
(元)与采购量 (斤)之间的关系如图,且采购单价不低于4元/斤.
(斤)之间的关系如图,且采购单价不低于4元/斤.
 万元,这列货车挂A型车厢
万元,这列货车挂A型车厢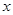 节,试写出
节,试写出
 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
 名学生去旅行,甲、乙旅行社的收费分别为
名学生去旅行,甲、乙旅行社的收费分别为 ,
, (m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2),D(a,-1).直线 轴于点N(3,0),与一次函数和反比例 函数的图象分别交于点B,C.