题目内容
平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=- x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
(1)求直线l2的解析式;
(2)设直线l1与l2相交于点M,问:是否存在这样的直线l:y=x+t,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上若存在,求出直线l的解析式;若不存在,请说明理由;
(3)设直线l2与x轴的交点为A,与y轴的交点为B,以点C(0, )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
①在如图所示的直角坐标系中画出图形;
②设OD=x,△BOD的面积为S1,△BEC的面积为S2,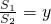 ,求y与x之间的函数关系式
,求y与x之间的函数关系式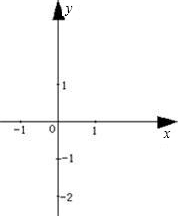 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围.
 解:(1)∵将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
解:(1)∵将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.∴折痕是直线y=-x,
∵直线l1的解析式为y=-
 x+1,
x+1,∴该直线与x轴交于点(
 ,0),与y轴交于点(0,1),
,0),与y轴交于点(0,1),∴l2点(0,-
 ),(-1,0),
),(-1,0),设l2解析式为y=kx-
 ,
,则有0=-k-
 ,即k=-
,即k=- ,
,∴l2的解析式为y=-
 x-
x- ;
;(2)因为直线l1与l2相交于点M,
∴
 ,
,∴
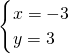 ,即M(-3,3),
,即M(-3,3),∵将坐标纸沿直线l折叠,点M恰好落在x轴上,
∴设M的对应点为N(a,0),则l:y=x+t过MN的中点F(
 ),
),∴
 ,即a=6-2t,
,即a=6-2t,∵y=x+t,与x轴交于E(-t,0),ME=NE,
∴(-3+t)2+32=(a+t)2,
∴t=3,即l的解析式为y=x+3;
(3)∵直线l2与x轴的交点为A,与y轴的交点为B,
∴A(-1,0),B(0,-
 ),
),∵以点C(0,
 )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方),
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方),∴OA=1,OB=1.5,OC=
 ,
,连接CA,
∵AO2=OC•OB,即
 ,
,∵∠AOC=∠AOB=90°,
∴△AOC∽△BOA,
∴∠CAO+∠BAO=∠ABO+∠BAO=90°,
∵CA是半径,
∴BA是⊙C的切线,
∴BA2=BD•BE,
∵在直角三角形AOB中,AB2=OA2+0B2=1+
 =
= ,
,∴BE=
 ,
,设D(a,b),∠DBO=α,
则S1=
 OB•|a|,S2=
OB•|a|,S2= BC•BE•sinα=
BC•BE•sinα= BC•BE•
BC•BE• •|a|,
•|a|,∴y=
 ,
,∵OB=
 ,BC=
,BC= ,
,∴y=
 =
= BD2,
BD2,∵BD2=DQ2+QB2=(
 +b)2+a2,a2+b2=x2,
+b)2+a2,a2+b2=x2,∴BD2=
 +x2+3b,
+x2+3b,∵CD2=CQ2+DQ2,
∴1+
 =a2+(
=a2+( -b)2,
-b)2,∴b=
 (x2-1),
(x2-1),∴y=
 (
( +x2+
+x2+ x2-
x2- ),
),即y=
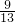 x2.
x2.分析:(1)因为将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.所以折痕是直线y=-x,然后利用直线l1与x轴交点(
 ,0),与y轴交点(0,1),求出l2过点(0,-
,0),与y轴交点(0,1),求出l2过点(0,- ),(-1,0),利用待定系数法即可求出解析式;
),(-1,0),利用待定系数法即可求出解析式;(2)因为直线l1与l2相交于点M,所以将两个函数的解析式联立,得到方程组,解之即可得到M(-3,3),又因将坐标纸沿直线l折叠,点M恰好落在x轴上,所以可设M的对应点为N(a,0),则l:y=x+t过MN的中点F(
 ),进而利用解析式可求出a=6-2t,求出y=x+t与x轴交于E(-t,0),利用ME=NE,结合两点间的距离公式即可列出方程(-3+t)2+32=(a+t)2,即可求出l的解析式为y=x+3;
),进而利用解析式可求出a=6-2t,求出y=x+t与x轴交于E(-t,0),利用ME=NE,结合两点间的距离公式即可列出方程(-3+t)2+32=(a+t)2,即可求出l的解析式为y=x+3;(3)因为直线l2与x轴的交点为A,与y轴的交点为B,所以可求A(-1,0),B(0,-
 ),又因以点C(0,
),又因以点C(0, )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方),所以OA=1,OB=1.5,OC=
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方),所以OA=1,OB=1.5,OC= ,连接CA,利用AO2=OC•OB,∠AOC=∠AOB=90°,可证△AOC∽△BOA,从而有∠CAO+∠BAO=∠ABO+∠BAO=90°,即可求出BA是⊙C的切线,利用切割线定理可得BA2=BD•BE,利用勾股定理可得AB 2=
,连接CA,利用AO2=OC•OB,∠AOC=∠AOB=90°,可证△AOC∽△BOA,从而有∠CAO+∠BAO=∠ABO+∠BAO=90°,即可求出BA是⊙C的切线,利用切割线定理可得BA2=BD•BE,利用勾股定理可得AB 2= ,两者结合可得BE=
,两者结合可得BE= .
.再设D(a,b),∠DBO=α,则S1=
 OB•|a|,S2=
OB•|a|,S2= BC•BE•sinα=
BC•BE•sinα= BC•BE•
BC•BE• •|a|,y=
•|a|,y= ,代入相关数据可得y=
,代入相关数据可得y= =
= BD2,再利用勾股定理得到BD2=DQ2+QB2=(
BD2,再利用勾股定理得到BD2=DQ2+QB2=( +b)2+a2,a2+b2=x2,CD2=CQ2+DQ2,代入相关数据可得:b=
+b)2+a2,a2+b2=x2,CD2=CQ2+DQ2,代入相关数据可得:b= (x2-1),y=
(x2-1),y= (
( +x2+
+x2+ x2-
x2- ).
).点评:本题需仔细分析题意,结合图形,利用切线的有关性质、勾股定理、待定系数法即可解决问题.

练习册系列答案
相关题目
 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围. 平面直角坐标系内有两条直线l1、l2,直线l1的解析式为
平面直角坐标系内有两条直线l1、l2,直线l1的解析式为 x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合. )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)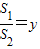 ,求y与x之间的函数关系式,并写出自变量x的取值范围.
,求y与x之间的函数关系式,并写出自变量x的取值范围.