题目内容
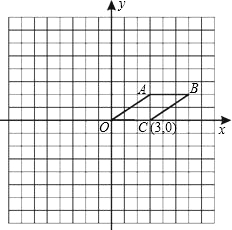
 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.(1)画出四边形OABC关于点O对称的四边形OA1B1C1,并写出点B1的坐标是
(-6,-2)
(-6,-2)
.(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2,并写出点B2的坐标是
(2,-6)
(2,-6)
.(3)在第(2)问的条件下,点B旋转到点B2所经过的弧BB2的长为
| 10 |
| 10 |
分析:(1)根据网格结构找出点A、B、C关于原点O对称的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点B1的坐标;
(2)根据网格结构找出点A、B、C绕点O顺时针方向旋转90°的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标;
(3)利用勾股定理列式求出OB,再根据弧长公式列式计算即可得解.
(2)根据网格结构找出点A、B、C绕点O顺时针方向旋转90°的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标;
(3)利用勾股定理列式求出OB,再根据弧长公式列式计算即可得解.
解答: 解:(1)四边形OA1B1C1如图所示,点B1(-6,-2);
解:(1)四边形OA1B1C1如图所示,点B1(-6,-2);
(2)四边形OA2B2C2如图所示,点B2(2,-6);
(3)由勾股定理得,OB=
=2
,
所以,点B旋转到点B2所经过的弧BB2的长=
=
π.
故答案为:(-6,-2);(2,-6);
π.
 解:(1)四边形OA1B1C1如图所示,点B1(-6,-2);
解:(1)四边形OA1B1C1如图所示,点B1(-6,-2);(2)四边形OA2B2C2如图所示,点B2(2,-6);
(3)由勾股定理得,OB=
| 22+62 |
| 10 |
所以,点B旋转到点B2所经过的弧BB2的长=
90•π•2
| ||
| 180 |
| 10 |
故答案为:(-6,-2);(2,-6);
| 10 |
点评:本题考查了利用旋转变换作图,弧长的计算,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 坐标系.
坐标系. 如图所示,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点即正方形的顶点,在这个4×4的方格纸中,找出格点C,使△ABC的面积为1个平方单位的三角形的个数是( )
如图所示,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点即正方形的顶点,在这个4×4的方格纸中,找出格点C,使△ABC的面积为1个平方单位的三角形的个数是( ) 已知,△ABC在方格纸中的位置如图所示,每个小方格的边长为1.
已知,△ABC在方格纸中的位置如图所示,每个小方格的边长为1. 如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.