题目内容
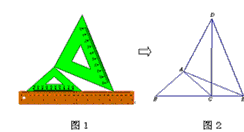
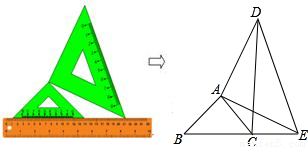
 将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.
将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.求证:△ABE≌△ACD.
分析:题中两个三角形均为等腰直角三角形,所以可得其腰相等,再加上一个角相等,即可证明其全等.
解答:证明:∵△ABC和△ADE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90,
即∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD.
∴AB=AC,AD=AE,∠BAC=∠DAE=90,
即∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
|
∴△ABE≌△ACD.
点评:本题考查了全等三角形的判定;熟练掌握全等三角形的判定方法,把实际问题转化为数学问题是一种能力,要注意培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

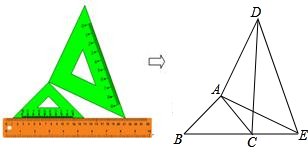
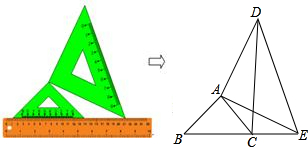 将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.
将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连接DC.