题目内容
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
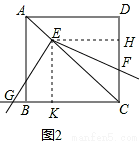
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;
(1)证明见解析;(2)是,证明见解析.
【解析】
试题分析:(1)由四边形ABCD是正方形,点E与点A重合,易证得ED=EB,∠D=∠EBG=90°,又由∠GEF=90°,利用同角的余角相等,即可得∠BEG=∠DEF,然后利用ASA即可判定△BEG≌△DEF,则可证得EF=EG;
(2)首先过点E作EH⊥CD于H,作EK⊥BC于K,易证得四边形EKCH是正方形,同(1)即可证得△GEK≌△FEH,证得EF=EG.
试题解析:(1)证明:∵四边形ABCD是正方形,点E与点A重合,
∴ED=EB,∠D=∠EBG=90°,
∵∠GEF=90°,
∴∠BEG+∠BEF=∠BEF+∠DEF=90°,
∴∠BEG=∠DEF,
在△BEG和△DEF中,
 ,
,
∴△BEG≌△DEF(ASA),
∴EF=EG;
(2)成立.理由:
【解析】
过点E作EH⊥CD于H,作EK⊥BC于K,
∴∠EHC=∠EKC=90°,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠HCE=45°,
∴四边形EKCH是矩形,∠HEC=∠HCE=45°,
∴EH=CH,
∴四边形EKCH是正方形,
∴EH=EK,∠EHF=∠EKG=90°,
∵∠GEF=90°,
∴∠GEK+∠KEF=∠KEF+∠FEH=90°,
∴∠GEK=∠FEH,
在△GEK和△FEH中,
 ,
,
∴△GEK≌△FEH(ASA),
∴EF=EG.
考点:1.正方形的性质;2.全等三角形的判定与性质.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案
 是反比例函数,则m .
是反比例函数,则m .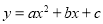 的部分对应值如下表:
的部分对应值如下表:













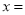 1
1 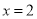 对应的函数值
对应的函数值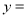 -8
-8 



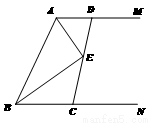
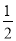 C.
C.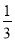 D.
D.