题目内容
如图:
1.BO、CO分别平分∠ABC和∠ACB,设∠A=n°(n为已知数)求∠O的度数;
2.BO、CO分别是⊿ABC两外角的平分线,设∠A=n°(n为已知数)求∠O的度数;
3.BO、CO分别平分∠ABC和∠ACD,设∠A=n°(n为已知数)求∠O的度数;

1.∠O=90°+![]() n°
n°
2.∠O=90°-![]() n°
n°
3.∠O= n°
n°
解析:(1)在三角形ABC中,![]() 因为BO、CO分别平分∠ABC和∠ACB,所以
因为BO、CO分别平分∠ABC和∠ACB,所以![]() ,根据三角形内角和∠O=90°+
,根据三角形内角和∠O=90°+![]() n°
n°
(2))∵BO、CO为△ABC两外角∠DBC、∠BCE的平分线∠A为n°,
∴∠BCO=![]() (∠A+∠ABC),∠OBC=
(∠A+∠ABC),∠OBC=![]() (∠A+∠ACB),∴∠BOC=180°-∠BCO-∠OBC=180°-
(∠A+∠ACB),∴∠BOC=180°-∠BCO-∠OBC=180°-  [∠A+(A+∠ABC+∠ACB)]=180°-
[∠A+(A+∠ABC+∠ACB)]=180°- ![]() (∠A+180°)=90°-
(∠A+180°)=90°-![]() n°;
n°;
(3)根据角平分线的定义得∠ACD=2∠OCD,∠ABC=2∠OBC,由三角形外角的性质有∠OCD=BOC+∠OBC,∠ACD=∠ABC+∠A,则2∠BOC+2∠OBC=∠ABC+∠A,即可得到∠BOC=![]() ∠A=
∠A= n°.
n°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
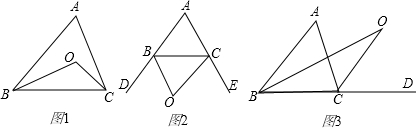

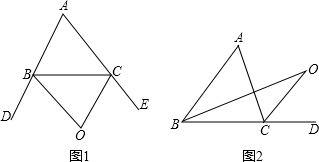 角平分线,若∠A=x°,求∠BOC的度数.
角平分线,若∠A=x°,求∠BOC的度数. 如图,AO=BO,CO=DO,AD与BC交于E,则图中全等三角形的对数为( )
如图,AO=BO,CO=DO,AD与BC交于E,则图中全等三角形的对数为( )
