Question

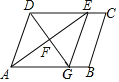
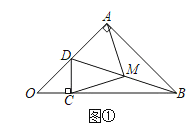
【题目】等腰直角三角形OAB中，∠OAB＝90°，OA＝AB，点D为OA中点，DC⊥OB，垂足为C，连接BD，点M为线段BD中点，连接AM、CM，如图①．

（1）求证：AM＝CM；

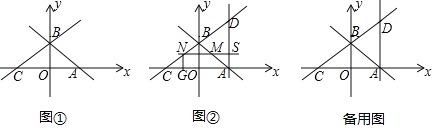
（2）将图①中的△OCD绕点O逆时针旋转90°，连接BD，点M为线段BD中点，连接AM、CM、OM，如图②．

①求证：AM＝CM，AM⊥CM；

②若AB＝4，求△AOM的面积．

Answer 1

【答案】（1）见解析；（2）①见解析，②2

【解析】

（1）直接利用直角三角形斜边的中线等于斜边的一半，即可得出结论；

（2）①延长CM交OB于T，先判断出△CDM≌△TBM得出CM＝TM，DC＝BT＝OC，进而判断出△OAC≌△BAT，得出AC＝AT，即可得出结论；

②先利用等腰直角三角形的性质求出再求出OD，DC＝CO＝，再用勾股定理得出CT，进而判断出CM＝AM，得出AM＝OM，进而求出ON，再根据勾股定理求出MN，即可得出结论．

解：（1）证明：∵∠OAB＝90°，

∴△ABD是直角三角形，

∵点M是BD的中点，

∴AM＝BD，

∵DC⊥OB，

∴∠BCD＝90°，

∵点M是BD的中点，

∴CM＝BD，

∴AM＝CM；

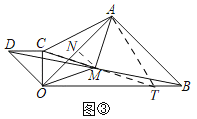
（2）①如图②，

在图①中，∵AO＝AB，∠OAB＝90°，

∴∠ABO＝∠AOB＝45°，

∵DC⊥OB，

∴∠OCD＝90°，

∴∠ODC＝∠AOB，

∴OC＝CD，

延长CM交OB于T，连接AT，

由旋转知，∠COB＝90°，DC∥OB，

∴∠CDM＝∠TBM，

∵点M是BD的中点，

∴DM＝BM，

∵∠CMD＝∠TMB，

∴△CDM≌△TBM（ASA），

∴CM＝TM，DC＝BT＝OC，

∵∠AOC＝∠BOC﹣∠AOB＝45°＝∠ABO，

∵AO＝AB，

∴△OAC≌△BAT（SAS），

∴AC＝AT，∠OAC＝∠BAT，

∴∠CAT＝∠OAC+∠OAT＝∠BAT+∠OAT＝∠OAB＝90°，

∴△CAT是等腰直角三角形，

∵CM＝TM，

∴AM⊥CM，AM＝CM；

②如图③，在Rt△AOB中，AB＝4，

∴OA＝4，OB=＝AB＝4，

在图①中，点D是OA的中点，

∴OD＝OA＝2，

∵△OCD是等腰直角三角形，

∴DC＝CO＝ODsin45°=＝，

由①知，BT＝CD，

∴BT＝，

∴OT＝OB﹣TB＝3，

在Rt△OTC中，CT＝＝2，

∵CM＝TM＝CT＝＝AM，

∵OM是Rt△COT的斜边上的中线，

∴OM＝CT＝，

∴AM＝OM，

过点M作MN⊥OA于N，则ON＝AN＝OA＝2，

根据勾股定理得，MN＝＝1，

∴S△AOM＝OAMN＝×4×1＝2．