Question

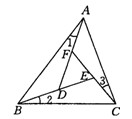20、△ABC中，∠1=∠2=∠3，图中有相似三角形吗？请说明理由．

Answer 1

分析：此题考查了相似三角形的判定，解题时要认真审题，选择适宜的判定方法．△DEF和△ABC中，∠DEF=∠2+∠BCE，而∠ACB=∠3+∠BCE，可得出∠DEF=∠ACB，同理可证得∠AFE=∠ABC，由此可证得△DEF∽△ABC．

解答：解：有，△DEF∽△BAC；理由如下：
∵∠CFD=∠3+∠FAC，
又∵∠1=∠3，
∴∠CFD=∠BAC．
同理可得：∠FED=∠ACB，
∴△DEF∽△BAC．

点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．