题目内容
当x=-2010时,求(| x |
| x+1 |
| x+1 |
| x2-1 |
| x2+1 |
| x2+x |
分析:把(
+
)÷
化为最简分式的形式,然后代入求值即可.
| x |
| x+1 |
| x+1 |
| x2-1 |
| x2+1 |
| x2+x |
解答:解:(
+
)÷
,
=
×
,
=
×
,
=
.
当x=-2010时,原式=
=
=
.
| x |
| x+1 |
| x+1 |
| x2-1 |
| x2+1 |
| x2+x |
=
| x(x-1)+x+1 |
| (x+1)(x-1) |
| x2+x |
| x2+1 |
=
| x2+1 |
| (x+1)(x-1) |
| x(x+1) |
| x2+1 |
=
| x |
| x-1 |
当x=-2010时,原式=
| x |
| x-1 |
| -2010 |
| -2010-1 |
| 2010 |
| 2011 |
点评:本题考查了分式的化简求值,比较容易,关键是把所求分式化为最简分式,然后再代入求值.

练习册系列答案
相关题目
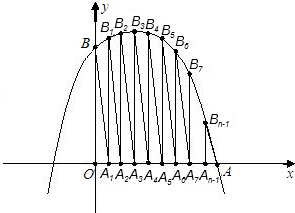 S2、S3、S4、…、Sn.
S2、S3、S4、…、Sn.