题目内容
11.-2$\sqrt{6}$<-3$\sqrt{2}$(比较大小).分析 首先分别求出-2$\sqrt{6}$、-3$\sqrt{2}$的平方各是多少;然后根据两个负数,哪个数的平方越大,则这个数就越小,判断出-2$\sqrt{6}$、-3$\sqrt{2}$的大小关系即可.
解答 解:${(-2\sqrt{6})}^{2}$=24,${(-3\sqrt{2})}^{2}$=18,
∵24>18,
∴${(-2\sqrt{6})}^{2}$>${(-3\sqrt{2})}^{2}$,
∴-2$\sqrt{6}$<-3$\sqrt{2}$.
故答案为:<.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键是判断出-2$\sqrt{6}$、-3$\sqrt{2}$的平方的大小关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在实数范围内,下列结论正确的是( )
| A. | 若|a|=|b|,则a=b | B. | 若a2=b2,则a=b | C. | 若$\root{3}{-a}=\root{3}{b}$,则a=-b | D. | 若a2>b2,则a>b |
19.把下列方程化成一般形式后,系数和为0的方程是( )
| A. | x2-2x+3=0 | B. | x2+2x-3=0 | C. | x2-4x-3=0 | D. | 2x2-5=3x |
20.方程(m-2)x|m|+3mx+1=0是关于x的一元二次方程,则( )
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
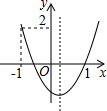 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴,给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1;⑤3a+2b<-1.其中正确结论的序号是②③④.
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴,给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1;⑤3a+2b<-1.其中正确结论的序号是②③④.