题目内容
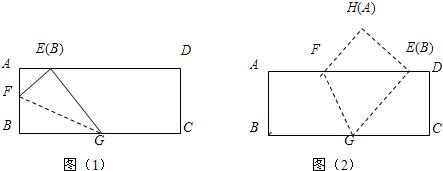
 长方形纸片ABCD中,AB=8cm,BC=4cm,现将纸片折叠,使点B与点D重合,GF为折痕.若FC=3cm,则GD=
长方形纸片ABCD中,AB=8cm,BC=4cm,现将纸片折叠,使点B与点D重合,GF为折痕.若FC=3cm,则GD=5cm
5cm
.分析:由折叠的性质得到GB=GD,设DG=GB=xcm,得到AG=AB-GB=(8-x)cm,再由AD=BC=4cm,在直角三角形ADG中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出GD的长.
解答:解:由折叠的性质得到GB=GD,设DG=GB=xcm,得到AG=AB-GB=(8-x)cm,
∵长方形ABCD中,AD=BC=4cm,
∴在Rt△ADG中,利用勾股定理得:AD2+AG2=DG2,即16+(8-x)2=x2,
整理得:16x=80,
解得:x=5,
则GD=5cm.
故答案为:5cm
∵长方形ABCD中,AD=BC=4cm,
∴在Rt△ADG中,利用勾股定理得:AD2+AG2=DG2,即16+(8-x)2=x2,
整理得:16x=80,
解得:x=5,
则GD=5cm.
故答案为:5cm
点评:此题考查了翻折变换(折叠问题),涉及的知识有:勾股定理,长方形的性质,熟练运用勾股定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
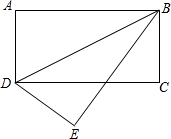 在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE=
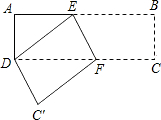
在如图的长方形纸片ABCD中,将△ABD沿BD折叠,点A落在点E处若∠ABD=35°,则∠CDE= 如图所示,已知长方形纸片ABCD中,沿着直线EF折叠,求作四边形EFCD关于直线EF的对称图形.(不要求写作法)
如图所示,已知长方形纸片ABCD中,沿着直线EF折叠,求作四边形EFCD关于直线EF的对称图形.(不要求写作法)