题目内容
 (2013•襄阳)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
(2013•襄阳)如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.(1)求证:DP∥AB;
(2)若AC=6,BC=8,求线段PD的长.
分析:(1)连结OD,由AB为⊙O的直径,根据圆周角定理得AB为⊙O的直径得∠ACB=90°,再由ACD=∠BCD=45°,则∠DAB=∠ABD=45°,所以△DAB为等腰直角三角形,所以DO⊥AB,根据切线的性质得OD⊥PD,于是可得到DP∥AB;
(2)先根据勾股定理计算出AB=10,由于△DAB为等腰直角三角形,可得到AD=
=5
;由△ACE为等腰直角三角形,得到AE=CE=
=3
,在Rt△AED中利用勾股定理计算出DE=4
,则CD=7
,易证得∴△PDA∽△PCD,得到
=
=
=
,所以PA=
PD,PC=
PD,然后利用PC=PA+AC可计算出PD.
(2)先根据勾股定理计算出AB=10,由于△DAB为等腰直角三角形,可得到AD=
| AB | ||
|
| 2 |
| AC | ||
|
| 2 |
| 2 |
| 2 |
| PD |
| PC |
| PA |
| PD |
| AD |
| CD |
5
| ||
7
|
| 5 |
| 7 |
| 7 |
| 5 |
解答:(1)证明:连结OD,如图,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠ABD=45°,
∴△DAB为等腰直角三角形,
∴DO⊥AB,
∵PD为⊙O的切线,
∴OD⊥PD,
∴DP∥AB;
(2)解:在Rt△ACB中,AB=
=10,
∵△DAB为等腰直角三角形,
∴AD=
=
=5
,
∵AE⊥CD,
∴△ACE为等腰直角三角形,
∴AE=CE=
=
=3
,
在Rt△AED中,DE=
=
=4
,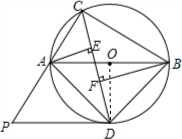
∴CD=CE+DE=3
+4
=7
,
∵∠PDA=∠PCD,∠P=∠P,
∴△PDA∽△PCD,
∴
=
=
=
,
∴PA=
PD,PC=
PD,
而PC=PA+AC,
∴
PD+6=
PD,
∴PD=
.
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠ACB的平分线交⊙O于点D,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠ABD=45°,
∴△DAB为等腰直角三角形,
∴DO⊥AB,
∵PD为⊙O的切线,
∴OD⊥PD,
∴DP∥AB;
(2)解:在Rt△ACB中,AB=
| AC2+BC2 |
∵△DAB为等腰直角三角形,
∴AD=
| AB | ||
|
| 10 | ||
|
| 2 |
∵AE⊥CD,
∴△ACE为等腰直角三角形,
∴AE=CE=
| AC | ||
|
| 6 | ||
|
| 2 |
在Rt△AED中,DE=
| AD2-AE2 |
(5
|
| 2 |

∴CD=CE+DE=3
| 2 |
| 2 |
| 2 |
∵∠PDA=∠PCD,∠P=∠P,
∴△PDA∽△PCD,
∴
| PD |
| PC |
| PA |
| PD |
| AD |
| CD |
5
| ||
7
|
∴PA=
| 5 |
| 7 |
| 7 |
| 5 |
而PC=PA+AC,
∴
| 5 |
| 7 |
| 7 |
| 5 |
∴PD=
| 35 |
| 4 |
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了圆周角定理定理、等腰直角三角形的性质和三角形相似的判定与性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 (2013•襄阳)如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为( )
(2013•襄阳)如图,BD平分∠ABC,CD∥AB,若∠BCD=70°,则∠ABD的度数为( ) (2013•襄阳)如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( )
(2013•襄阳)如图,平行四边形ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则平行四边形ABCD的两条对角线的和是( ) (2013•襄阳)如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为
(2013•襄阳)如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为 (2013•襄阳)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为
(2013•襄阳)如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为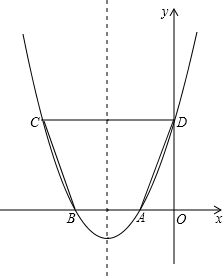 (2013•襄阳)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x=-2.
(2013•襄阳)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x=-2.