Question

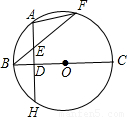
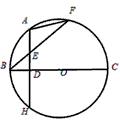
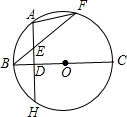
已知：如图所示，BC为圆O的直径，A、F是半圆上异于B、C的一点，D是BC上的一点，BF交AH于点E，A是弧BF的中点，AH⊥BC．
（1）求证：AE=BE；
（2）如果BE•EF=32，AD=6，求DE、BD的长．

Answer 1

解：（1）连接AB；
∵BC是直径，且BC⊥AH，
∴；
∵A是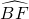的中点，
∴==；
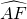∴∠BAE=∠ABE；
∴AE=BE；

（2）易知DH=AD=6；
∴AE=6-DE，EH=6+DE；
由相交弦定理，得：AE•EH=BE•EF，即：
（6-DE）（6+DE）=32，解得DE=2；
Rt△BDE中，BE=AE=AD-DE=4，DE=2；
由勾股定理，得：BD==2．
分析：（1）求AE=BE，可证它们的所对的角相等；连接AB、通过证弧AF、弧AB、弧BH都相等，来得到∠BAE=∠EBA，从而证得AE=BE的结论．
（2）已知了AD的长即可得出HD的长，可用DE表示出AE、EH，然后由相交弦定理可求出DE的值，进而可在Rt△BDE中，由勾股定理求出BD的长．
点评：此题主要考查了圆周角定理、垂径定理、相交弦定理的综合应用能力．