Question

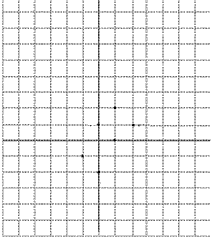在图上建立直角坐标系，用线段顺次连结点（0，0），（1，3），（4，4），（4，0），（0，0）．
（1）这是一个什么图形？
（2）求出它的面积；
（3）求出它的周长．

Answer 1

考点：坐标与图形性质,三角形的面积

专题：

分析：（1）根据平面直角坐标系找出各点的位置，然后顺次连接即可；
（2）根据四边形的面积等于一个直角三角形的面积加上一个梯形的面积计算即可得解；
（3）利用勾股定理和四边形的周长公式列式计算即可得解．

解答：解：（1）如图，是四边形；

（2）面积=

1

2

×1×3+

1

2

×（3+4）×3，
=

3

2

+

21

2

，
=12；

（3）由勾股定理得，

12+32

=

10

，
所以，周长=2

10

+4+4=2

10

+8．

点评：本题考查了坐标与图形性质，主要利用了在平面直角坐标系中确定点的位置是方法，三角形的面积，勾股定理，需熟记．