题目内容
已知:反比例函数y=-
.
(1)若将反比例函数y=-
的图象绕原点O旋转90°,求所得到的双曲线C的解析式并画图;
(2)双曲线C上是否存在到原点O距离为
的点P?若存在,求出点P的坐标.
| 6 |
| x |
(1)若将反比例函数y=-
| 6 |
| x |
(2)双曲线C上是否存在到原点O距离为
| 13 |
分析:(1)建立网格平面直角坐标系,然后利用描点法作出反比例函数y=-
的图象,然后找出绕点O旋转90°后的对应点,再描点连线作出函数图象即可;
(2)根据函数解析式设出点P的坐标为(a,
),然后利用勾股定理列式进行计算即可得解.
| 6 |
| x |
(2)根据函数解析式设出点P的坐标为(a,
| 6 |
| a |
解答: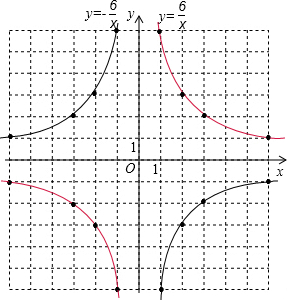 解:(1)建立平面直角坐标系如图,如图所示,红色的双曲线即为双曲线C,
解:(1)建立平面直角坐标系如图,如图所示,红色的双曲线即为双曲线C,
反比例函数y=-
上的点(-2,3)绕点O顺时针旋转90°后对应的点为(3,2),
所以,双曲线C的解析式为y=
;
(2)设点P坐标为(a,
),
则a2+(
)2=
2,
整理得,a4-13a2+36=0,
解得a2=4或a2=9,
解得a1=2,a2=-2,a3=3,a4=-3,
所以
=3,
=-3,
=2,
=2,
所以点P的坐标为(2,3)或(-2,-3)或(3,2)或(-3,-2).
 解:(1)建立平面直角坐标系如图,如图所示,红色的双曲线即为双曲线C,
解:(1)建立平面直角坐标系如图,如图所示,红色的双曲线即为双曲线C,反比例函数y=-
| 6 |
| x |
所以,双曲线C的解析式为y=
| 6 |
| x |
(2)设点P坐标为(a,
| 6 |
| a |
则a2+(
| 6 |
| a |
| 13 |
整理得,a4-13a2+36=0,
解得a2=4或a2=9,
解得a1=2,a2=-2,a3=3,a4=-3,
所以
| 6 |
| 2 |
| 6 |
| -2 |
| 6 |
| 3 |
| 6 |
| -3 |
所以点P的坐标为(2,3)或(-2,-3)或(3,2)或(-3,-2).
点评:本题考查了利用旋转变换作图,反比例函数图象,以及反比例函数图象上点的坐标特征,作出网格平面直角坐标系是解题的关键.

练习册系列答案
相关题目
 (2012•昌平区二模)如图,已知:反比例函数
(2012•昌平区二模)如图,已知:反比例函数