Question

如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE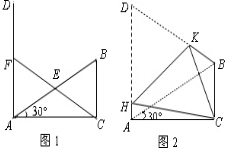并延长交AD于F，若AB=2．
（1）直接写出BC的长；
（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．

Answer 1

分析：（1）根据直角三角形中30°的角所对的边是斜边的一半可直接进行解答；
（2）先根据BC=1可求出AC的长，再根据△ABD是等边三角形可知AD=2，由图形折叠的性质可知CH=DH，设DH=x，在Rt△ACH中利用勾股定理即可求出x的值，由锐角三角函数的定义即可求解．

解答：解：（1）∵△ABC中，∠ACB=90°，∠CAB=30°，AB=2，
∴BC=

1

2

AB=1；

（2）由（1）得BC=1，
∴AC=

3

，
∵△ABD是等边三角形，
∴AD=2，
设DH=x，由折叠得：DH=CH=x，
∴在Rt△ACH中，
由勾股定理得：（2-x）²+3=x²，
解得：x=

7

4

∴sin∠ACH=

AH

CH

=

1

7

．

点评：本题考查的是图形翻折变换的性质、勾股定理、等边三角形的性质及锐角三角函数的定义，解答此题的关键是熟知图形折叠的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．