题目内容
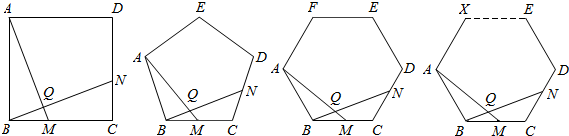
将已知六边形ABCDEF，用对角线将它剖分成互不重叠的4个三角形，那么各种不同的剖分方法种数是
- A.6
- B.8
- C.12
- D.14
D
分析：要用对角线将六边形ABCDEF剖分成互不重叠的4个三角形，①通过同一个顶点作三条对角线，所以有六种作法．②从一个顶点作两条对角线；③中间是个四边形，两端2个三角形，把四边形加条对角线．
解答：
解：∵六边形ABCDEF有6个顶点，且用对角线将它剖分成互不重叠的4个三角形，
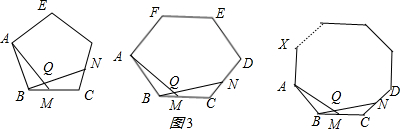
∴只能通过同一个顶点作三条对角线（如图1），这种分法有6种，
也从一个顶点作两条对角线（如图2），这种分法有2种，
如图3，中间是个四边形，两端2个三角形，把四边形加条对角线，这种分法有6种，
故各种不同的剖分方法有14种．
故选D．
点评：本题考查了多边形的性质，n边形过一个顶点有（n-3）条对角线，它们把n边形分割成了（n-2）个三角形．
分析：要用对角线将六边形ABCDEF剖分成互不重叠的4个三角形，①通过同一个顶点作三条对角线，所以有六种作法．②从一个顶点作两条对角线；③中间是个四边形，两端2个三角形，把四边形加条对角线．
解答：
解：∵六边形ABCDEF有6个顶点，且用对角线将它剖分成互不重叠的4个三角形，∴只能通过同一个顶点作三条对角线（如图1），这种分法有6种，
也从一个顶点作两条对角线（如图2），这种分法有2种，
如图3，中间是个四边形，两端2个三角形，把四边形加条对角线，这种分法有6种，
故各种不同的剖分方法有14种．
故选D．
点评：本题考查了多边形的性质，n边形过一个顶点有（n-3）条对角线，它们把n边形分割成了（n-2）个三角形．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
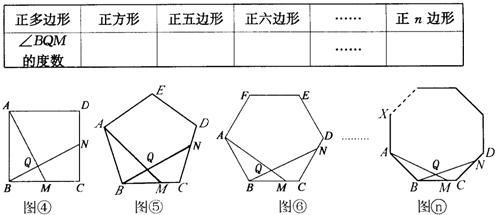
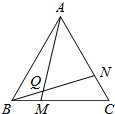（1）已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，∠BAM=∠NBC，猜想∠BQM等于多少度，并证明你的猜想．
