题目内容
11. 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )| A. | 函数的对称轴是直线x=1 | B. | 当x<2时,y随x的增大而减小 | ||
| C. | 函数的开口方向向上 | D. | 函数图象与y轴的交点坐标是(0,-3) |
分析 利用二次函数的解析式与图象,判定开口方向,求得对称轴,与y轴的交点坐标,进一步利用二次函数的性质判定增减性即可.
解答 解:∵y=x2-2x-3=(x-1)2-4,
∴对称轴为直线x=1,
又∵a=1>0,开口向上,
∴x<1时,y随x的增大而减小,
令x=0,得出y=-3,
∴函数图象与y轴的交点坐标是(0,-3).
因此错误的是B.
故选:B.
点评 本题考查了二次函数的性质,抛物线与坐标轴的交点坐标,掌握二次函数的性质是解决本题的关键

练习册系列答案
相关题目
16.若-5x2ym与xny是同类项,则方程nx-m=7的解是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.已知:∠A=25°12′,∠B=25.12°,∠C=25.2°,下列结论正确的是( )
| A. | ∠A=∠B | B. | ∠B=∠C | C. | ∠A=∠C | D. | 三个角互不相等 |
 如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.
如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.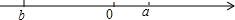 已知有理数a,b在数轴上的位置如图所示.
已知有理数a,b在数轴上的位置如图所示.