题目内容
 如图,点A是双曲线
如图,点A是双曲线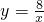 (x>0)上的一点,P为x轴正半轴上的一点,且点P的坐标为(4,0),将A点绕P点顺时针旋转90°,恰好落在此双曲线上的另一点B,则B点的坐标为________.
(x>0)上的一点,P为x轴正半轴上的一点,且点P的坐标为(4,0),将A点绕P点顺时针旋转90°,恰好落在此双曲线上的另一点B,则B点的坐标为________.
(4+2 ,4-2
,4-2 )
)
分析:过A,B作x轴的垂线,垂足分别是M,N.易证△AMP≌△BNP,则根据A,B的坐标都满足函数解析式即可求解.
解答: 解:过A,B作x轴的垂线,垂足分别是M,N.
解:过A,B作x轴的垂线,垂足分别是M,N.
易证△AMP≌△BNP.
∴AM=PN,PM=BN,
设A的坐标为( ,m),
,m),
∴OM= ,AM=m.
,AM=m.
则MP=4- .
.
∴ON=OP+PN=4+AM=4+m.
BN=MP=4- .
.
则B的坐标是(4+m,4- ).
).
代入双曲线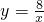 得到:(4+m)(4-
得到:(4+m)(4- )=8
)=8
解得:m=2 ,
,
则ON=4+m=4+2 ,BN=4-
,BN=4- =4-2
=4-2 ,
,
则B的坐标是(4+2 ,4-2
,4-2 ).
).
故答案是:(4+2 ,4-2
,4-2 ).
).
点评:本题是反比例函数与等腰三角形的性质,全等三角形的性质的综合应用,正确理解A,B坐标之间的关系是解决本题的关键.
 ,4-2
,4-2 )
)分析:过A,B作x轴的垂线,垂足分别是M,N.易证△AMP≌△BNP,则根据A,B的坐标都满足函数解析式即可求解.
解答:
 解:过A,B作x轴的垂线,垂足分别是M,N.
解:过A,B作x轴的垂线,垂足分别是M,N.易证△AMP≌△BNP.
∴AM=PN,PM=BN,
设A的坐标为(
 ,m),
,m),∴OM=
 ,AM=m.
,AM=m.则MP=4-
 .
.∴ON=OP+PN=4+AM=4+m.
BN=MP=4-
 .
.则B的坐标是(4+m,4-
 ).
).代入双曲线
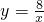 得到:(4+m)(4-
得到:(4+m)(4- )=8
)=8解得:m=2
 ,
,则ON=4+m=4+2
 ,BN=4-
,BN=4- =4-2
=4-2 ,
,则B的坐标是(4+2
 ,4-2
,4-2 ).
).故答案是:(4+2
 ,4-2
,4-2 ).
).点评:本题是反比例函数与等腰三角形的性质,全等三角形的性质的综合应用,正确理解A,B坐标之间的关系是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,点A是双曲线
如图,点A是双曲线 (2013•萧山区模拟)如图,点P是双曲线
(2013•萧山区模拟)如图,点P是双曲线 如图,点P是双曲线y=
如图,点P是双曲线y= (2013•南通二模)如图,点A是双曲线y=
(2013•南通二模)如图,点A是双曲线y= 如图,点M是双曲线y=
如图,点M是双曲线y=