题目内容
在等腰△ABC中,一腰上的高为
,这条高与底边的夹角的正弦值为
,求△ABC的面积.
| 3 |
| ||
| 2 |
考点:解直角三角形
专题:
分析:画出图形,易求得∠ACD=30°,根据特殊角三角函数值即可求得AC的长,根据等腰三角形腰长相等性质即可求得△ABC的面积.
解答:解:画出图形,

∵sin∠BCD=
,
∴∠BCD=60°,
∴∠B=30°,
∴∠C=30°,∠ACD=30°,
∴AB=AC=
CD=1,
∴S=
AB•CD=
.

∵sin∠BCD=
| ||
| 2 |
∴∠BCD=60°,
∴∠B=30°,
∴∠C=30°,∠ACD=30°,
∴AB=AC=
| 2 | ||
|
∴S=
| 1 |
| 2 |
| ||
| 4 |
点评:本题考查了直角三角形中三角函数的运用,考查了特殊角的三角函数值,本题中求AB的长是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,某公路路基横截面为梯形,按工程设计要求路面宽度为10,路基高度为5.8m,坡BC的坡比是1:0.8,求路基下底宽和∠B的度数.
如图,某公路路基横截面为梯形,按工程设计要求路面宽度为10,路基高度为5.8m,坡BC的坡比是1:0.8,求路基下底宽和∠B的度数. 如图,已知锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
如图,已知锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.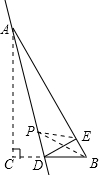 如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,AB=2,将△ABC沿直线AD翻折,使点C落AB边上的点E处.若点P是直线AD上的动点,则PE+PB的最小值是
如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,AB=2,将△ABC沿直线AD翻折,使点C落AB边上的点E处.若点P是直线AD上的动点,则PE+PB的最小值是 已知如图,在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M.
已知如图,在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M.