题目内容
8.(1)已知二次函数y=x2-mx+m的图象与x轴只有一个公共点,求m的值;(2)已知二次函数y=x2-2x-3a的图象与两坐标轴只有一个公共点,求a的取值范围.
分析 (1)利用△=b2-4ac=0时,抛物线与x轴有1个交点得到△=(-m)2-4m=0,然后解关于m的一元二次方程即可;
(2)由于二次函数y=x2-2x-3a的图象的顶点不是原点,则可判断抛物线与x轴没有公共点,利用△=b2-4ac<0时,抛物线与x轴没有交点得到△=(-2)2-4•(-3a)<0,然后解关于a的不等式即可.
解答 解:(1)根据题意得△=(-m)2-4m=0,
解得m=0或m=4;
(2)因为二次函数y=x2-2x-3a的图象与两坐标轴只有一个公共点,
所以抛物线与x轴没有公共点,
所以△=(-2)2-4•(-3a)<0,
解得a<-$\frac{1}{3}$.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
16.下列各式计算结果正确是( )
| A. | -3+3=-6 | B. | -6÷2×3=-1 | C. | -9÷(-1$\frac{1}{2}$)2=-4 | D. | -4+(-2)×$\frac{1}{2}$=-3 |
13.下列算式正确的是( )
| A. | $\sqrt{9}=3$ | B. | $\sqrt{4}=±2$ | C. | $\sqrt{0.9}=0.3$ | D. | $\sqrt{{{({-2})}^2}}=-2$ |
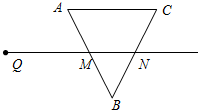 如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒).
如图,射线QN与边长为8的等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN.动点P从点Q出发,沿射线QN以每秒2cm的速度向右移动,以点P为圆心,2$\sqrt{3}$cm为半径的圆也随之移动.若AM=MB=4cm,QM=8cm,且经过t秒,当⊙P与△ABC的边相切时,则t可取的一切值为t=2或3≤t≤7或t=8(单位:秒). 如图所示,已知长方形的长为a米,宽为b米,半圆半径为r米.
如图所示,已知长方形的长为a米,宽为b米,半圆半径为r米.