Question

已知：图1为一锐角是30°的直角三角尺，其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等)．操作：将三角尺移向直径为4cm的⊙O，它的内Rt△ABC的斜边AB恰好等于⊙O的直径，它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。

思考：

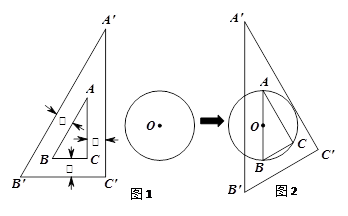
1.求直角三角尺边框的宽

2.求证：BB′C′+CC′B′=75°。

3.求边B′C′的长。

 

Answer 1

 

1.过O作OD⊥A′C′于D，交AC于E，

∵AC∥A′C′，

∴AC⊥OD，

∵A′C′与⊙O相切，AB为圆O的直径，且AB=4cm，

∴OD=OA=OB=AB=×4=2（cm），

在Rt△AOE中，∠A=30°，

∴OE=OA=×2=1（cm），

∴DE=OD-OE=2-1=1（cm）

则三角尺的宽为1cm．（4分

2.∵三角板的宽度是一样大

∴BB′平分∠A′B′C′，C C′平分∠A′C′B′

∵∠A′B′C′=60°，∠A′C′B′=90°

∴BB′C′=30°，CC′B′=45°

∴BB′C′+CC′B′=75°（3分）

3.B′C=.（3分）

解析:（1）OD为圆的半径，利用Rt△AOE中，∠A=30°，算出OE的长，这样就求出DE的长，即为三角尺的宽；

（2）根据三角形的宽度相等得出BB′、CC′是角平分线算出BB′C′、CC′B′的值，然后证出结论；

（3）利用三角函数性质计算出B′C的值