题目内容
19.计算与化简:(1)计算:2×(-1)3-5÷$\frac{1}{2}$×2;
(2)计算:-24÷[1-(-3)2]+($\frac{2}{3}$-$\frac{3}{5}$)×(-1.5);
(3)-5(a2-2)•4a-8•6(a2-2a);
(4)2m-3[3m-(2n-m)]•2n.
分析 (1)先算乘方,再算乘除,最后算减法;
(2)先算乘方和乘法,再算乘法,最后算加减即可;
(3)先算乘法,再合并同类项即可;
(4)先算括号里面的,再算乘法,最后合并即可.
解答 解:(1)2×(-1)3-5÷$\frac{1}{2}$×2
=2×(-1)-5×2×2
=-2-20
=-22;
(2)-24÷[1-(-3)2]+($\frac{2}{3}$-$\frac{3}{5}$)×(-1.5)
=-16÷[1-9]+$\frac{2}{3}$×(-$\frac{3}{2}$)-$\frac{3}{5}$×(-$\frac{3}{2}$)
=-16÷(-8)-1+$\frac{9}{10}$
=2-1+$\frac{9}{10}$
=1$\frac{9}{10}$;
(3)-5(a2-2)•4a-8•6(a2-2a)
=-20a3+40a-48a2+96a
=-20a3-48a2+136a;
(4)2m-3[3m-(2n-m)]•2n
=2m-3[3m-2n+m]•2n
=2m-6n[4m-2n]
=2m-24mn+12n2.
点评 本题考查了整式的混合运算和求值的应用,主要考查学生的化简能力,注意运算顺序,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.我县城市居民用电收费方式有以下两种:
估计小明家下月总用电量为200度,
(1)若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
(2)请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
(3)到下月付费时,小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
| 类别 | 普通电价 | 峰谷分时电价 | |
| 时间 | 每度0.52元 | 峰时(8;00-21:00) | 谷时(21:00-8:00) |
| 电价 | 每度0.55元 | 每度0.30元 | |
(1)若其中峰时电量为50度,则小明家按照哪种方式付电费比较合适?能省多少元?
(2)请你帮小明计算,峰时电量为多少度时,两种方式所付的电费相等?
(3)到下月付费时,小明发现那月总用电量为200度,用峰谷电价付费方式比普通电价付费方式省了14元,求那月的峰时电量为多少度?
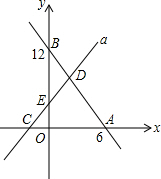 如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.
如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.