题目内容
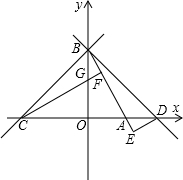
已知直线y=-| 3 |
| 3 |
求：（1）点C的坐标；
（2）图象经过A、B、C三点的二次函数的解析式．
分析：（1）先设点C的坐标是（x，0），分别令x=0、y=0，求出A、B点的坐标，再利用两点之间距离公式可得（1-0）2+（0-
）2=（x-1）2+02，求解即可求C点坐标；
（2）先设所求二次函数的解析式是y=ax2+bx+c，然后分别把（1，0）、（0，
）、（3，0）以及（1，0）、（0，
）、（-1，0）代入函数，可得三元一次方程组，求解即可．
| 3 |
（2）先设所求二次函数的解析式是y=ax2+bx+c，然后分别把（1，0）、（0，
| 3 |
| 3 |
解答：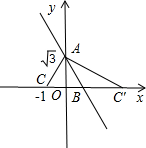
解：（1）设点C的坐标是（x，0），根据题意得
当x=0时，y=
；
当y=0时，x=1；
∴A点坐标是（1，0），B点坐标是（0，
），
∴（1-0）2+（0-
）2=（x-1）2+02，
解得x=3或-1，
∴C点坐标是（3，0）或（-1，0）；
（2）设所求二次函数的解析式是y=ax2+bx+c，
把（1，0）、（0，
）、（3，0）代入函数得
，
解得
，
∴所求函数解析式是y=
x2-
x+
；
把（1，0）、（0，
）、（-1，0）代入函数得
，
解得
，
∴所求函数解析式是y=-
x2+
．
故所求的二次函数的解析式是y=
x2-
x+
或y=-
x2+
．
解：（1）设点C的坐标是（x，0），根据题意得当x=0时，y=
| 3 |
当y=0时，x=1；
∴A点坐标是（1，0），B点坐标是（0，
| 3 |
∴（1-0）2+（0-
| 3 |
解得x=3或-1，
∴C点坐标是（3，0）或（-1，0）；
（2）设所求二次函数的解析式是y=ax2+bx+c，
把（1，0）、（0，
| 3 |
|
解得
|
∴所求函数解析式是y=
| ||
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
把（1，0）、（0，
| 3 |
|
解得
|
∴所求函数解析式是y=-
| 3 |
| 3 |
故所求的二次函数的解析式是y=
| ||
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
点评：本题考查了一次函数的性质、待定系数法求函数解析式、解三元一次方程组．解题的关键是运用坐标系内两点之间距离的公式．
练习册系列答案
相关题目
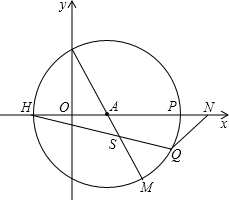
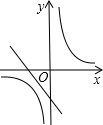已知直线y=-3x+m和双曲线y=| k |
| x |
| A、①② | B、②③ | C、③④ | D、①④ |
已知直线y=3x-2与两条坐标轴围成的三角形面积是（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
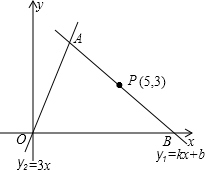点B．设点A的横坐标为m（m＞1且m≠5）．
