题目内容
5. 已知:如图,一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点,且D点坐标为(1,0).
已知:如图,一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点,且D点坐标为(1,0).(1)求二次函数的表达式及C点的坐标;
(2)观察图象,直接写出下面小题的答案:不等式$\frac{1}{2}$x2+bx+c>$\frac{1}{2}$x+1的解集为x<0或x>4;
(3)在抛物线的对称轴上是否存在点P,使得PC+PE的值最小?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)求出点B的坐标,然后将点B、D的坐标代入二次函数解析式,求出b、c的值,然后求出一次函数和二次函数的交点C的坐标;
(2)根据图象可得,当不等式$\frac{1}{2}$x2+bx+c>$\frac{1}{2}$x+1时,解集为x<0或x>4;
(3)根据题意可得,点D、E关于二次函数的对称轴对称,连接CD与对称轴的交点即为点P使PC+PE的值最小.
解答 解:(1)∵一次函数y=$\frac{1}{2}$x+1与y轴的交点为B,
令x=0,可得y=1,
∴B(0,1),
将B(0,1),D(1,0)的坐标代入y=$\frac{1}{2}$x2+bx+c得,
$\left\{\begin{array}{l}{c=1}\\{b+c+\frac{1}{2}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=1}\end{array}\right.$,
∴解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x+1,
∵二次函数的图象与一次函数的图象交于B、C两点,
∴$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=3}\end{array}\right.$,
∴C(4,3);
(2)由图可得,当x<0或x>4时,不等式$\frac{1}{2}$x2+bx+c>$\frac{1}{2}$x+1;
故答案为:x<0或x>4.
(3)∵点D和点E关于x=$\frac{3}{2}$对称,
连接DC与对称轴的交点即为符合条件的点P,使PC+PE的值最小,
设直线CD的解析式为y=kx+m,
则$\left\{\begin{array}{l}{4k+m=3}\\{k+m=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{m=-1}\end{array}\right.$,
∴解析式为:y=x-1,
当x=$\frac{3}{2}$时,y=$\frac{1}{2}$,
∴点P的坐标为($\frac{3}{2}$,$\frac{1}{2}$).
点评 此题考查了二次函数的综合应用,涉及了利用待定系数法求二次函数和一次函数解析式、函数图象交点坐标以及轴对称-最短路径问题等知识,难度适中.

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 3+3$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$+$\sqrt{6}$ |
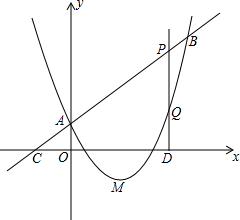 已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合).
已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合).