题目内容
“解方程x4-6x2+5=0”,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设x2=y,那么,x4=y2,于是原方程可变化为y2-6y+5=0,解这个方程,得:y1=1,y2=5.当y1=1时,x2=1,所以x=±1,当y2=5时,x2=5,所以x=±![]() .所以原方程共有四个根:x1=-1,x2=1,x3=-
.所以原方程共有四个根:x1=-1,x2=1,x3=-![]() ,x4=
,x4=![]() .仿照上面的方法解方程(x2-x)2-4(x2-x)-12=0,若设x2-x=y,则原方程可化为________,原方程的根为________.
.仿照上面的方法解方程(x2-x)2-4(x2-x)-12=0,若设x2-x=y,则原方程可化为________,原方程的根为________.
答案:
解析:
解析:
|
y2-4y-12=0,x1=-2,x2=3 |

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
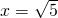 .所以原方程有四个根:x1=1,x2=-1,x3=
.所以原方程有四个根:x1=1,x2=-1,x3= ,x4=-
,x4=-