题目内容
5．已知：实数x、y满足$\sqrt{x-y+8}+（y+1）^{2}$=0．（1）求x与y的值；
（2）求xy的平方根及x-y的立方根．
分析 （1）根据非负数的性质列出方程求出x、y的值；
（2）分别求出xy和x-y的值，根据平方根和立方根的概念解答即可．
解答 解：（1）由题意得，x-y+8=0，y+1=0，
解得x=-9，y=-1；
（2）xy=9，
9的平方根是±3，
x-y=-8，
-8的立方根是-2．
答：xy的平方根是±3，x-y的立方根-2．
点评 本题考查的是非负数的性质、平方根和立方根的概念，掌握几个非负数的和为0时，这几个非负数都为0是解题的关键．
练习册系列答案
相关题目
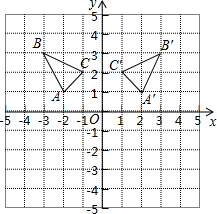如图是一个的正方形格纸，△ABC中A点坐标为（-2，1）．
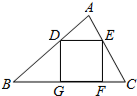如图，△ABC中，点D、E是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形，若DE=2cm，求△ABC的面积．