��Ŀ����
��֪���ı���ABCD�������Σ���P��ֱ��BC�ϣ���G��ֱ��AD�ϣ�P��G���������ζ����غϣ�����CD��ͬ�ࣩ��PD=PG��DF��PG�ڵ�H����ֱ��AB�ڵ�F�����߶�PG�Ƶ�P��ʱ����ת90��õ��߶�PE������EF.
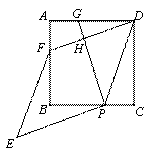
(1)��ͼ1������P���G�ֱ����߶�BC���߶�AD��ʱ.
����֤��DG=2PC��
����֤���ı���PEFD�����Σ�
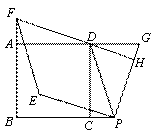
(2)��ͼ2������P���G�ֱ����߶�BC���߶�AD���ӳ�����ʱ��������ı���PEFD�������������ı��Σ���֤����IJ���.
 |  | ||
��1��
��֤������ͼ1
 ��PM��AD�ڵ�M
��PM��AD�ڵ�M
��PD=PG��
��MG=MD��
�֡�MD=PC
��DG=2PC
��֤������PG��FD��H
���DGH+��ADF= 90�� ��25�� ͼ1
�֡ߡ�ADF+��AFD= 90��
���DGP=��AFD
���ı���ABCD�������Σ�PM��AD�ڵ�M��
 ���A=��PMD= 90�㣬PM=AD��
���A=��PMD= 90�㣬PM=AD��
���PMG�ա�DAF
��DF=PG
��PG=PE
��FD=PE��
��DF��PG��PE��PG
��DF��PE
���ı���PEFD��ƽ���ı���.
�֡�PE=PD
����PEFD������
��2���ı���PEFD������
֤������ͼ��
���ı���ABCD�������Σ�DH��PG��H
���ADC=��DHG=90��
���CDG=��DHG=90��
���CDP+��PDG=90�㣬��GDH+��G=90��
��PD=PG
���PDG=��G
���CDP=��GDH
���CDP=��ADF
�֡�AD=DC����FAD=��PCD=90��
���PCD�ա�FAD
��FD=PD
�� PD=PG=PE
��FD=PE
�֡�FD��PG��PE��PG
��FD��PE
���ı���PEFD��ƽ���ı���.
�֡�FD=PD
����PEFD������

�ı���ABCD�У��Խ���AC��BD���ڵ�O���������������ж�����ı�����ƽ���ı��ε��ǣ�������
| �� | A�� | OA=OC��OB=OD | B�� | AD��BC��AB��DC | C�� | AB=DC��AD=BC | D�� | AB��DC��AD=BC |
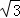 ��AD=1����CD��CE�ij�����ע�⣺�����еļ�����̺ͽ�����������ţ�
��AD=1����CD��CE�ij�����ע�⣺�����еļ�����̺ͽ�����������ţ�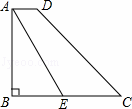
 ������װ��12���������ɸ��������dz���ɫ��ͬ�⣬�������ͬ���������������һ�����ǰ���ĸ�����
������װ��12���������ɸ��������dz���ɫ��ͬ�⣬�������ͬ���������������һ�����ǰ���ĸ�����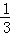 �������ĸ���Ϊ��������
�������ĸ���Ϊ��������