题目内容
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠BCD=45°,点E在BC上,且∠AEB=60°.若AB=2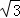 ,AD=1,求CD和CE的长.(注意:本题中的计算过程和结果均保留根号)
,AD=1,求CD和CE的长.(注意:本题中的计算过程和结果均保留根号)
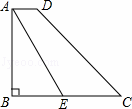
解:过点D作DF⊥BC,
∵AD∥BC,∠ABC=90°,
∴四边形ABFD为矩形,
∵∠BCD=45°,
∴DF=CF,
∵AB=2 ,
,
∴DF=CF=2 ,
,
∴由勾股定理得CD=2 ;
;
∵AD=1,
∴BF=1,
∴BC=2 +1,
+1,
∵∠AEB=60°,
∴tan60°= ,
,
∴ =
= ,
,
∴BE=2,
∴CE=BC﹣BE=2 +1﹣2=2
+1﹣2=2 ﹣1.
﹣1.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B. +(
+( ﹣1)0﹣
﹣1)0﹣ 的值为( )
的值为( )




 ﹣
﹣ =0的解为x=
=0的解为x=  D.
D. 
 与x轴之间的一个动点,且点M是抛物线
与x轴之间的一个动点,且点M是抛物线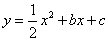 的顶点,则方程
的顶点,则方程 的解的个数是( )
的解的个数是( )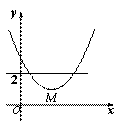
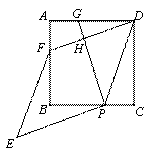
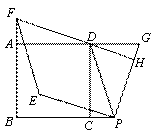
 (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .