题目内容
设△ABC的三边长分别为BC=2,CA=3,AB=4,ha,hb,hc分别表示边BC、CA、AB上的高,则 =
=
- A.

- B.
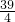
- C.

- D.

B
分析:根据三角形的面积公式列出关于ha,hb,hc间的关系式 BC•ha=
BC•ha= CA•hb=
CA•hb= AB•hc,然后求得它们之间的数量关系,将这种数量关系代入化简
AB•hc,然后求得它们之间的数量关系,将这种数量关系代入化简 后的代数式并求值.
后的代数式并求值.
解答:∵△ABC的三边长分别为BC=2,CA=3,AB=4,ha,hb,hc分别表示边BC、CA、AB上的高,
∴ BC•ha=
BC•ha= CA•hb=
CA•hb= AB•hc,即2ha=3hb=4hc;
AB•hc,即2ha=3hb=4hc;
故设2ha=3hb=4hc=t(t>0),则ha= ,hb=
,hb= ,hc=
,hc= ,
,
∴ =(
=( +
+ +
+ )(
)( +
+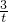 +
+ )=
)= •
• =
=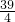 ,即
,即 =
=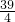 .
.
故选B.
点评:本题考查了三角形的面积.解答此类题目,可以利用比例的基本性质将ha,hb,hc间的数量关系解答出来.
分析:根据三角形的面积公式列出关于ha,hb,hc间的关系式
 BC•ha=
BC•ha= CA•hb=
CA•hb= AB•hc,然后求得它们之间的数量关系,将这种数量关系代入化简
AB•hc,然后求得它们之间的数量关系,将这种数量关系代入化简 后的代数式并求值.
后的代数式并求值.解答:∵△ABC的三边长分别为BC=2,CA=3,AB=4,ha,hb,hc分别表示边BC、CA、AB上的高,
∴
 BC•ha=
BC•ha= CA•hb=
CA•hb= AB•hc,即2ha=3hb=4hc;
AB•hc,即2ha=3hb=4hc;故设2ha=3hb=4hc=t(t>0),则ha=
 ,hb=
,hb= ,hc=
,hc= ,
,∴
 =(
=( +
+ +
+ )(
)( +
+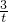 +
+ )=
)= •
• =
=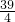 ,即
,即 =
=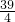 .
.故选B.
点评:本题考查了三角形的面积.解答此类题目,可以利用比例的基本性质将ha,hb,hc间的数量关系解答出来.

练习册系列答案
相关题目
设a,b,c分别是△ABC的三边长,且
=
,则它的内角∠A、∠B的关系是( )
| a |
| b |
| a+b |
| a+b+c |
| A、∠B>2∠A |
| B、∠B=2∠A |
| C、∠B<2∠A |
| D、不确定 |


 ,则它的内角∠A、∠B的关系是( )
,则它的内角∠A、∠B的关系是( )