题目内容
在三角形ABC中AB<AC<BC,若在BC上存在一点D,使把这三角形沿AD剪开后的两个三角形相似,且较大的三角形面积是较小三角形面积的2倍,则AB:AC:BC=
- A.1:
 :
:
- B.1:2:3
- C.1:4:9
- D.以上答案均不对
A
分析:根据题意,△ABD∽△CAD,∠B与∠CAD,∠C与∠BAD是对应角,所以△ABC是直角三角形,所以,设BD为x,则CD为2x,再分别表示出AB、AC,比值可求.
解答: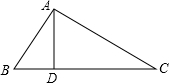 解:∵△ABD与△ACD相似,
解:∵△ABD与△ACD相似,
∴∠B=∠CAD,∠C=∠BAD,
∴AD⊥BC,
设BD为x,则CD为2x,
根据射影定理,得AB2=BD•BC=x•3x,AC2=CD•BC,
∴AB= x,AC=
x,AC= x,
x,
∴AB:AC:BC= x:
x: x:3x=1:
x:3x=1: :
: .
.
故选A.
点评:本题考查相似三角形的定义,运用射影定理求解.
分析:根据题意,△ABD∽△CAD,∠B与∠CAD,∠C与∠BAD是对应角,所以△ABC是直角三角形,所以,设BD为x,则CD为2x,再分别表示出AB、AC,比值可求.
解答:
 解:∵△ABD与△ACD相似,
解:∵△ABD与△ACD相似,∴∠B=∠CAD,∠C=∠BAD,
∴AD⊥BC,
设BD为x,则CD为2x,
根据射影定理,得AB2=BD•BC=x•3x,AC2=CD•BC,
∴AB=
 x,AC=
x,AC= x,
x,∴AB:AC:BC=
 x:
x: x:3x=1:
x:3x=1: :
: .
.故选A.
点评:本题考查相似三角形的定义,运用射影定理求解.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在三角形ABC中AB<AC<BC,若在BC上存在一点D,使把这三角形沿AD剪开后的两个三角形相似,且较大的三角形面积是较小三角形面积的2倍,则AB:AC:BC=( )
A、1:
| ||||
| B、1:2:3 | ||||
| C、1:4:9 | ||||
| D、以上答案均不对 |
 10、如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是( )
10、如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是( )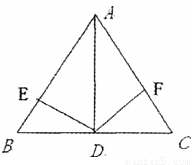
 :
:
 :
: